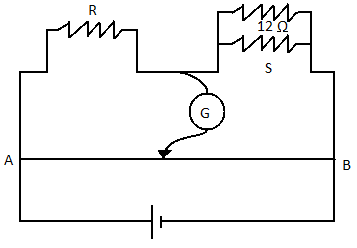
In a metre bridge the null point is found at a distance of 40cm from $A$. If a resistance of $12\Omega $ is connected in parallel with $S$, the null point occurs at $50cm$ from $A$. Determine value of $R$ and $S$.

Hint: Here two conditions are given, in one condition a resistance of $12\Omega $ is connected in parallel to $S$ and in another condition there is no such resistance connected in parallel. Applying the condition of Wheatstone bridge in these two conditions will give two different linear equations in form of variables of $R$ and $S$ . After solving the two equations you will get the answer.

Complete step by step solution:
Here in this question two conditions are given,
First, when a resistance of $12\Omega $ is not connected in parallel to $S$ . In that case we can write,
$\dfrac{R}{S} = \dfrac{{{l_1}}}{{(100 - {l_1})}}$
Putting ${l_1} = 40cm$ as given in the question we have,
$\dfrac{R}{S} = \dfrac{{40}}{{100 - 40}}$
So the relation between $R$ and $S$ is given by,
$R = \dfrac{2}{3}S$

Now case second when $12\Omega $ resistance is connected in parallel to the resistor $S$ .
In this case the effective resistance can be written as,
$\dfrac{1}{{{S_1}}} = \dfrac{1}{S} + \dfrac{1}{{12}}$
On simplifying this expression we have,
$\dfrac{1}{{{S_1}}} = \dfrac{{12 + 5}}{{12S}}$
Taking reciprocals on both sides we have,
${S_1} = \dfrac{{12S}}{{(12 + 5)}}$
Now writing the condition of Wheatstone bridge we have,
$\dfrac{R}{{{S_1}}} = \dfrac{{{l'}}}{{100 - {l'}}}$
Putting the expression for ${S_1}$ we have,
$R = \dfrac{{12S}}{{(12 + S)}} \times \dfrac{{50}}{{50}}$
On simplifying the above expression we have,
$R = \dfrac{{12S}}{{12 + S}}$
Now we have two expressions for $R$ after equating them we have,
$\dfrac{2}{3}S = \dfrac{{12S}}{{(12 + S)}}$
On simplifying the above expression we have,
$12 + S = 18$
So we have, $S = 6\Omega $
So we have $R = \dfrac{2}{3} \times 6 = 4\Omega $

So, the values of $R$ and $S$ are $4\Omega $ and $6\Omega $ respectively.

Note: It is important to note the working principle of a meter bridge. A meter bridge is an instrument that works on the principle of a Wheatstone bridge. A meter bridge is used in finding the unknown resistance of a conductor as that of in a Wheatstone bridge. The null point of a Wheatstone is also known as the balance point of the Wheatstone bridge.