




An Overview of Angle Properties of Circle
The circle is one of the most interesting and important chapters when it comes to geometry. Being an important elementary figure in the field of geometry, circles have many properties associated with them. These properties have great theoretical importance and also have interesting applications.
In this lesson, we will learn about some interesting properties of a circle. We will cover the cyclic and tangent properties of a circle and their theorems along with angle properties of circle questions and answers.
Cyclic Properties of Circle
Property 1: The angle inscribed in a semicircle is a right angle.
The angle subtended by a semicircle measures 90 degrees. In other words, this property states that if you join the endpoints of a semicircle on a third point somewhere on the circumference of the circle, the angle inscribed would be a right angle.

Reference image for property 1
Property 2: Inscribed angles subtended by the same arc are equal.

Inscribed Angles x and y
In the figure shown above, the arc AEC subtends two inscribed angles $\angle x$ and $\angle y$. Therefore, these two angles will be equal.
Property 3: Central angles subtended by arcs of the same length are equal in measure.
If there are two arcs in a circle that are equal in length, the central angles subtended by them are equal.

Reference image for property 3
Property 4: The central angle of a circle is twice any inscribed angle subtended by the same arc.

Reference image for property 4
As expressed in the image above, the central angle subtended by the arc is $2 \alpha$, and the inscribed angle subtended by the same arc is $\alpha$.
Property 5: Supplementary opposite angles
The opposite angles of a cyclic quadrilateral are supplementary. In other words, the sum of the measures of the opposite angles of a quadrilateral that is inscribed in a circle is equal to 180 degrees. In the figure below, $\angle \mathrm{A}+\angle \mathrm{C}=180^{\circ}$
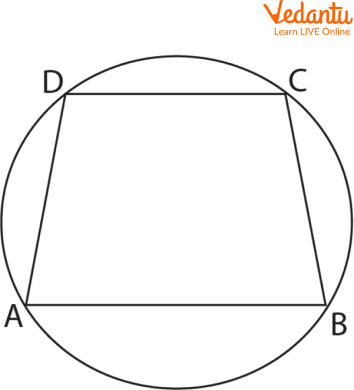
Reference image for property 5
Tangent Properties of Circle
Property 1: A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
If AB is a tangent that has P as a point of contact on the circle with centre O, segment OP will be perpendicular to the tangent AB.

Reference image for property 1
Property 2: When two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length.

Reference image for property 2
Solved Examples
Below are some angle properties of a circle questions and answers:
Q 1. In the figure given below, if the $\angle A D C=70^{\circ}$, what is the measure of $\angle A B C$?

Example 1
Ans: We know that the angle subtended by an arc is twice the angle subtended by it on the circumference.
From the figure, we know that
$\angle \mathrm{ADC}= 70^{\circ}$
So, we get
$\angle \mathrm{ABC}=2 \angle \mathrm{ADC}$
It can be written as
$\angle \mathrm{ABC}=2 \angle 70^{\circ}$
So, we get
$\angle \mathrm{ABC}=140^{\circ}$
Practice Questions
Q 1. The figure below shows a circle passing through points $A, B, C$, and $D$. The angle $\angle B A C=70^{\circ}$. What is the measure of $\angle DBC+\angle DCB$?

Image for Practice Question 1
Ans: $110^{\circ}$
Q 2. In the figure given below, $A C$ is the diameter of the circle. $A B=B C$ and $\angle A E D=118^{\circ}$. Find $\angle D A B$ ?
Image for Practice Question 2
Ans: $\angle D A B$ = $73^{\circ}$
Summary
In this article, we focused on one of the most important topics in the chapter on Circles. We learned numerous angle and cyclic properties of circles that helped us in understanding theorems. Not just that but we also covered all the angle and tangent properties of circles. To have better clarity about the application of the properties, we went through the angle properties of a circle worksheet, where we solved some examples using the properties. These properties and theorems are helpful in understanding and solving geometric problems.
FAQs on Angle and Tangent Properties of a Circle
1. What are the two fundamental properties of a tangent to a circle?
The two fundamental properties of a tangent in relation to a circle are:
- Perpendicularity to Radius: A tangent to a circle is always perpendicular (at a 90° angle) to the radius at the point of tangency.
- Equal Length from an External Point: If two tangent segments are drawn to a circle from the same external point, their lengths are equal.
2. What is the main angle property of a cyclic quadrilateral?
The most important angle property of a cyclic quadrilateral (a quadrilateral inscribed in a circle) is that its opposite angles are supplementary. This means that the sum of opposite angles is always equal to 180 degrees. For a quadrilateral ABCD inscribed in a circle, ∠A + ∠C = 180° and ∠B + ∠D = 180°.
3. How does a central angle relate to an inscribed angle subtended by the same arc?
A central angle is an angle whose vertex is at the centre of the circle, while an inscribed angle has its vertex on the circumference. For any given arc, the measure of the central angle is exactly twice the measure of any inscribed angle that subtends that same arc. For example, if an inscribed angle is 40°, the central angle for the same arc will be 80°.
4. Why is the angle in a semicircle always a right angle (90°)?
The angle in a semicircle is always 90° because it is an application of the central angle theorem. The arc of a semicircle corresponds to a straight line passing through the centre, which forms a central angle of 180°. Since the inscribed angle is always half the central angle subtended by the same arc, the angle at the circumference will be half of 180°, which is exactly 90°.
5. What is the difference between the 'angle in the same segment' property and the 'angles subtended by the same arc' property?
These two properties describe the same geometric fact. An arc divides the circle into two segments (a major and a minor segment). The property that angles subtended by the same arc at the circumference are equal is the same as saying that angles in the same segment of a circle are equal. Both statements explain why, if you pick two different points on the major arc, the angles they form with the endpoints of the minor arc will be identical.
6. If two different arcs in a circle have the same length, what can be said about their central and inscribed angles?
If two arcs in a circle are equal in length, it means they are congruent. Consequently, the angles they subtend will also be equal. This applies to both types of angles:
- The central angles subtended by the equal arcs will be equal.
- The inscribed angles subtended by the equal arcs will also be equal to each other.
7. Can a quadrilateral have its opposite angles sum to 180° and still not be a cyclic quadrilateral?
No, this is not possible. The property that opposite angles are supplementary is a definitive condition for a quadrilateral to be cyclic. This is the converse of the cyclic quadrilateral theorem. If you can prove that either pair of opposite angles of a quadrilateral adds up to 180°, you have proven that all four of its vertices lie on the circumference of a single circle.









