Why Understanding Altitude Properties Matters in Geometry
Have you ever wondered what that line which falls perpendicular to either of the sides of a triangle is called? Or ever wondered if there can only be one of those lines in a figure or if there can be even more? These perpendicular lines coming from the vertex of any triangle and then falling perpendicularly on the opposite side are called altitude in mathematics. In this article, we will look at these altitudes, will also learn the geometrical property of altitudes, and at last will also learn what is an orthocentre of a triangle. Sounds interesting right? So let's start learning.
Altitude of a Triangle
What Is Altitude?
In a triangle, a particular Line segment which is drawn from its vertex and is connected to the opposite side of the triangle making a 90-degree inclination with that side is referred to as the altitude.
Triangles usually are of three kinds of obtuse, equilateral, and isosceles triangles.
In each type of triangle, the property of their altitude differs in various ways and usually is used to calculate the area of a triangle because the altitude is equivalent to the height of the triangle.
In an obtuse-angled triangle the altitude is present outside the main triangle body for which we have to extend the base of the triangle and then draw a perpendicular line segment from the opposite vertex touching the extended base
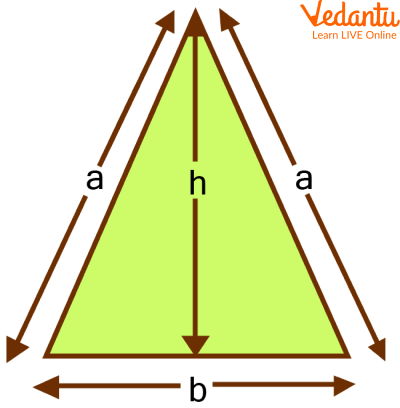
The altitude in an equilateral triangle interestingly divides the triangle into two equal parts.
The isosceles triangle altitude bisects the angle of the vertex and bisects the base. It should be noted that an isosceles triangle is a triangle with two congruent sides and so, the altitude bisects the base and vertex.

Altitude of an Obtuse-Angled Triangle
Properties of Altitude
Below are listed some properties of altitude:
There can only be a maximum of three altitudes inside or outside a triangle.
It is at a 90 degrees angle to the opposite side.
The altitude of a triangle can either be inside it or can also be outside it depending upon the type of triangle being talked about.
As we all know, there can only be a max of three altitudes inside a triangle. Therefore, the junction at which all those three altitudes meet is referred to as the orthocentre of a triangle.
Properties of Orthocentre
In this section of the article, we will discuss about the various properties of orthocenter:
As discussed in the above section a triangle can only have a maximum of three altitudes and the portion at which those three altitudes meet with one another is called an Orthocentre. Now we will look at the orthocenter of a triangle properties:

The point indicated as ‘O’ is the orthocentre of a right-angled triangle
For an acute angled Triangle, the orthocentre is drawn inside the triangle body.
For an obtuse-angled triangle, the orthocentre is drawn outside the triangle body
Whereas the orthocentre of a right-angled triangle is drawn at the vertices of the right angles.
Above were some unique orthocenters of a triangle properties.
Formulas to Calculate the Altitudes of Various Triangles
Geometrical Property of Altitudes
Below are listed the geometrical properties of altitudes
All of the altitudes in a triangle are concurrent or congruent.
The altitude of a triangle lies inside or outside the triangle.
Orthocentre can either lie inside or outside the triangle
Solved Examples
Below are some questions related to the altitude of a triangle:
Example 1: Calculate the altitude of a triangle having all equal sides of measure 6 cm.
Ans: According to the question the given triangle is an equilateral triangle
The formula for calculating the altitude of an equilateral triangle is $h=\dfrac{1}{2} \times \sqrt{3} \times s$ where $s$ is the length of the sides.
Therefore, $h=\dfrac{1}{2} \times \sqrt{3} \times 6$
$h=3 \sqrt{3} \mathrm{~cm}$
Example 2: Calculate the side of the equilateral triangle if the height or the altitude is 2cm.
Ans: For equilateral triangle
$h$ (height or altitude) $=\dfrac{1}{2} \times \sqrt{3} \times s$ where ' $s$ ' is the length of the side Given $h=2 \mathrm{~cm}$ noe putting the value in the equation we get
$(h \times 2) \div \sqrt{3}=s$
$(2 \times 2) \div \sqrt{3}=s$
Therefore, $\mathrm{s}=\dfrac{4}{\sqrt{3}} \mathrm{~cm}$
Practice Questions
Q 1. Write down all the formulas for finding altitude of the following triangles:
Right angle triangle
Isosceles triangle
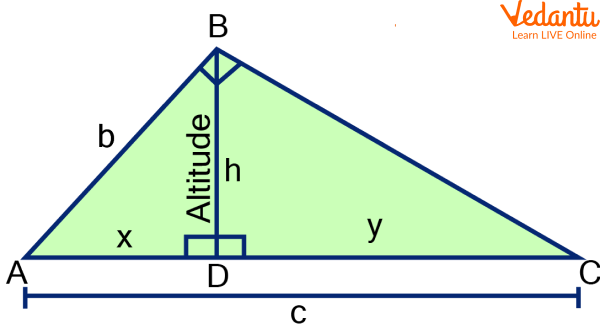
Ans: a. $h=\sqrt{x y}$
b. $h=\sqrt{a^2-\dfrac{b^2}{4}}$
Q 2. Find the measure of the altitude of a triangle having three equals sides of 8 cm
Ans: $4 \sqrt{3} \mathrm{~cm}$
Q 3. Calculate the height of a right angle triangle whose base values are $x=2 \mathrm{~cm}$ and $y=4 \mathrm{~cm}$
Ans: For right angle triangle $h=\sqrt{xy}$
Therefore, $h=\sqrt{2 \times 4}=2 \sqrt{2} \mathrm{~cm}$
Summary
To complete all the learnings from this article we can say that altitudes are the heights of a triangle and are usually used to calculate the area of the triangle. Altitudes can help us find and relate various triangle properties with each other for example congruency. Through this article, we learned about the basic properties of altitudes of the triangle and also looked at the positions of the altitudes. With this, we would like to end this article and hope that we were clear and understandable enough to clear all your doubts yet if you still have doubts you can write them down in the comment section below.
FAQs on Properties of Altitude: Definition, Examples & Applications
1. What is the definition of an altitude of a triangle in geometry?
In geometry, an altitude of a triangle is a perpendicular line segment drawn from a vertex to the line containing the opposite side. This opposite side is referred to as the 'base' of the triangle in relation to that specific altitude. Essentially, the altitude represents the height of the triangle from that vertex.
2. What are the most important properties of a triangle's altitudes?
The key properties of altitudes in a triangle are:
Every triangle has exactly three altitudes, one from each vertex.
An altitude is always perpendicular to the opposite side, forming a 90-degree angle.
The three altitudes of a triangle are concurrent, meaning they intersect at a single point called the orthocentre.
The location of the orthocentre depends on the type of triangle: inside for acute, outside for obtuse, and at the vertex of the right angle for a right-angled triangle.
3. What is the main difference between an altitude and a median of a triangle?
The main difference lies in their definition and function. An altitude is concerned with perpendicularity (height), as it must form a right angle with the opposite side. In contrast, a median is concerned with bisecting a side, as it connects a vertex to the midpoint of the opposite side. While they can be the same line in special cases (like in an equilateral triangle), their fundamental properties are distinct.
4. Does the altitude of a triangle always bisect the base?
No, the altitude does not always bisect the base. This is a common misconception. The altitude only bisects the base in two specific cases:
In an equilateral triangle, all three altitudes bisect their corresponding bases.
In an isosceles triangle, only the altitude drawn from the vertex angle (between the two equal sides) to the unequal base will bisect it.
In a scalene triangle, no altitude will bisect the base.
5. What is special about the altitudes in a right-angled triangle?
In a right-angled triangle, the altitudes have a unique property. Two of the altitudes are the legs (perpendicular sides) of the triangle itself. The third altitude is the one drawn from the vertex of the right angle to the hypotenuse. Consequently, the orthocentre (the intersection point of the three altitudes) is located at the vertex where the right angle is formed.
6. Why does the orthocentre lie outside the triangle for an obtuse triangle?
In an obtuse triangle, one angle is greater than 90 degrees. To draw a perpendicular line (altitude) from one of the acute-angled vertices to the opposite side, you must extend the line of the opposite side outside the triangle's boundary. Since at least two altitudes fall on these extended sides, their point of intersection, the orthocentre, must also lie outside the physical area of the triangle.
7. How is the length of an altitude calculated using the area of a triangle?
You can calculate the length of an altitude if you know the triangle's area and the length of the base corresponding to that altitude. The formula for the area of a triangle is Area = (1/2) × base × height. Since the altitude is the height, you can rearrange the formula to find the altitude: Altitude = (2 × Area) / base.
8. What is the formula to find the altitude of an equilateral triangle if you only know its side length?
For an equilateral triangle with a side length 'a', the formula to directly calculate the altitude (h) is h = (√3 / 2) × a. This formula is derived from the Pythagorean theorem, as the altitude in an equilateral triangle divides it into two congruent 30-60-90 right-angled triangles.
9. How can one differentiate between the orthocentre and the centroid of a triangle?
The key difference is the lines that form them. The orthocentre is the point where the three altitudes (perpendiculars from vertices to opposite sides) intersect. The centroid, on the other hand, is the point where the three medians (lines from vertices to the midpoints of opposite sides) intersect. While they are the same point in an equilateral triangle, in all other triangles they are distinct points with different geometric properties.