




How to Reflect a Point or Shape Across the Y Axis
Have you ever thought about how you would represent the reflection of a point in the y-axis? This is accomplished through the use of reflection in the y-axis concept. If you do not know about it, do not get worried, as this article covers all the concepts of reflection in the y-axis, and the graph xy = 1 is reflected in y = 2x using attractive images so that the children can easily grasp the topics. Let us now begin our learning.
What is the Reflection of a Point in the y-axis?
Reflection of a point in the y-axis states that the y-coordinate stays the same when a point is reflected across the y-axis, the x-coordinate is assumed to be the additive inverse of the given abscissa. For example, a point (x, y) is reflected across the y-axis as (-x, y).

Reflection of a point in the y-axis
A Point on the y-axis has Coordinates
A point on the y-axis has coordinates in the form of ordered pairs having the form (0, k), where k is the point on the y-axis. Here, 0 specifies the distance between the abscissa and the origin. When x = 0, the value of the y-axis can be anything, irrespective of the value of the abscissa.
Rules to Find the Reflection in the y-axis
There is no hard rule to find the reflection in the y-axis; you just need to follow these two simple steps, which are given below:
Keep the coordinates of the y-axis fixed
Reverse the sign of the x coordinate
The obtained value of the x coordinate and y coordinate is the reflection of a point on the y-axis.
Solved Examples
Q 1. Find the reflection of a point on the y-axis of the following:
(3, 5)
(3, -2)
Ans: For part 1, we need to follow the given steps:
Read the coordinates (3, 5) and find out in which quadrant it lies, i.e. 1st quadrant
Mark the values of x = 3 and y = 5 in the respective quadrants
Highlight the point and write its coordinates
To find its reflection, keep the ordinate same, i.e. 5, and take the additive inverse of the abscissa, i.e. -3
Now, choose the quadrant for the new coordinates, i.e. (-3, 5)
Place the values of x = -3 and y = 5 in the appropriate quadrant
Highlight the point and write its coordinates
This is how you find the reflection of a point (3, 5) on the y-axis.
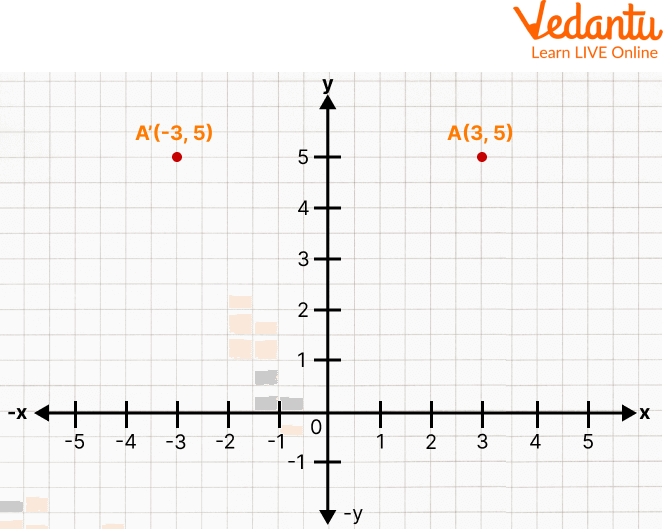
Reflection of a point in the y-axis
For part 2, we need to follow the given steps:
Read the coordinates (3, -2) and find out in which quadrant it lies, i.e. 4th quadrant
Mark the values of x = 3 and y = -2 in the respective quadrants
Highlight the point and write its coordinates
To find its reflection, keep the ordinate constant, i.e. -2, and take the additive inverse of the abscissa, i.e. -3
Now, choose the quadrant for the new coordinate, i.e. (-3, -2)
Mark the values of x = -3 and y = -2 in the appropriate quadrant
Highlight the point and write its coordinates
This is how you find the reflection of a point (3, -2) on the y-axis.

Reflection on the y-axis
A point on the y-axis of the following is 5 and -2, respectively, the same as the initial given problem.
Practice Problems
Q 1. Locate the reflection on the y-axis of the point (5,6).
Ans. (-5, 6)
Q 2. Find the reflection of a point on the y-axis of the following:
(a) (2, -3)
(b) (-3, 7)
Ans. (a) (-2, -3)
(b) (3, 7)
Q 3. Find the reflection on the y-axis of the points:
(a) (4, 5)
(b) (-1, -2)
Ans. (a) (-4, 5)
(b) (1, -2)
Summary
Summing up here with the concept of reflection in the y-axis. This writing describes all the topics, including rules to find the reflection, graph xy = 1 is reflected in y = 2x, a point on the y-axis has a coordinate, etc. Here we have discussed in depth how to solve the problem based on the reflection of a point in the y-axis. Some practice problems are assigned to the students along with their answers so that they can do more practice and gain proficiency in the concept.
FAQs on Reflection in Y Axis: Explained for Students
1. What is meant by reflection in the y-axis in coordinate geometry?
Reflection in the y-axis is a transformation that flips a point or a geometric figure across the vertical y-axis. In this process, the y-axis acts as a mirror. The resulting point, called the image, is at the same perpendicular distance from the y-axis as the original point, but on the opposite side.
2. What is the rule for finding the coordinates of a point after reflection in the y-axis?
The general rule for reflecting a point P(x, y) across the y-axis to get its image P'(x', y') is:
The x-coordinate (abscissa) changes to its additive inverse. So, x' = -x.
The y-coordinate (ordinate) remains the same. So, y' = y.
Therefore, the reflection of P(x, y) in the y-axis is P'(-x, y).
3. Can you give an example of reflecting a point in the y-axis?
Certainly. Let's take the point A(4, 5). To reflect this point in the y-axis, we apply the rule (x, y) → (-x, y).
The x-coordinate 4 becomes -4.
The y-coordinate 5 remains unchanged.
Thus, the reflection of point A(4, 5) in the y-axis is the point A'(-4, 5).
4. Why does only the x-coordinate change its sign during a reflection in the y-axis?
During a reflection in the y-axis, every point is moved horizontally to the opposite side of the axis. The y-axis itself is the line where x=0. The distance of a point (x, y) from the y-axis is its horizontal distance, which is determined by the absolute value of its x-coordinate. To move it to the other side of the mirror line (y-axis) while keeping the same distance, we must change its sign (e.g., from positive to negative or vice versa). The vertical position, determined by the y-coordinate, does not change as the reflection is purely horizontal.
5. How is the reflection of a point in the y-axis different from its reflection in the x-axis?
The key difference lies in which coordinate changes and which axis serves as the mirror:
Reflection in the y-axis: The y-axis acts as the mirror. The x-coordinate changes its sign, while the y-coordinate remains the same. The rule is P(x, y) → P'(-x, y).
Reflection in the x-axis: The x-axis acts as the mirror. The y-coordinate changes its sign, while the x-coordinate remains the same. The rule is P(x, y) → P''(x, -y).
6. What happens when a point lying on the y-axis itself is reflected in the y-axis?
If a point lies on the y-axis, its x-coordinate is zero, so its coordinates are of the form (0, y). When we apply the reflection rule (x, y) → (-x, y), the new coordinates become (-0, y), which is still (0, y). Therefore, any point on the line of reflection (the y-axis in this case) is an invariant point; its image is the same as the original point.
7. If the reflection of a point is (5, -3) in the y-axis, what were the original coordinates?
To find the original point (pre-image), we must reverse the reflection process. The rule for reflection in the y-axis is (x, y) → (-x, y). If the image is (5, -3), it means:
-x = 5, which implies the original x-coordinate was -5.
y = -3, which means the original y-coordinate was -3.
Therefore, the original coordinates of the point were (-5, -3).
8. Are there any real-world applications or examples of reflection in the y-axis?
Yes, reflection in the y-axis is a fundamental concept in various fields. For example:
In computer graphics and animation, it is used to create symmetrical objects or mirror characters and environments.
In design and architecture, the principle of symmetry, which is a form of reflection, is crucial for creating balanced and aesthetically pleasing structures.
In physics, particularly in optics, reflection principles are used to understand how images are formed by plane mirrors.















