




Key Properties and Tricks for Seven Circle Theorems
In geometry, we examine several circle theorems related to the various elements of a circle, including a chord, segments, etc. Let's first define a circle before moving on to talk about the circle theorems. A circle is a closed, two-dimensional figure where every point in the plane is equally spaced from a central point. The fixed point and fixed distance are both referred to as the centre and radius, respectively. We will examine many circle theorems used in geometry to address a variety of issues in this article.
History of the Euclid
Ancient Greek mathematician Euclid was a logician and geometer. The Elements book, often regarded as the "father of geometry," laid the theoretical groundwork for the discipline's development up until the early 19th century.

Euclid "Father of Geometry" (300 BCE)
Name: Euclid
Born: Around 325 BC
Died: Around 265 BC
Field: Mathematics
Nationality: Greek
What are the Seven Circle Theorems?
The statements of the seven circle theorems are:
A chord's angle at its centre is twice as large as its angle at its circumference.
The diameter at the circumference forms a right angle with the surrounding plane.
The angles that the same arc subtends at its circumference are equal.
At the circle's centre, two equal chords subtend two equal angles.
Two chords are equal if the angles they subtend at the centre are also equal.
In a cyclic quadrilateral, the opposing angles are supplementary.
At the point of contact, there is a 90-degree angle between the radius and the tangent.
Circle Theorems Proofs
Let's prove some of the crucial circle theorems we covered above in this part.
Theorem 1: A chord's angle at its centre is twice as large as its angle at its circumference.
Proof: Take a look at the circle below, where an arc (or segment) AB subtends ∠AOB at the circle's centre O and ∠ACB at a point on its circumference. We must demonstrate that $\angle AOB = 2 \times \angle ACB$. As shown, draw a line segment across points O and C and allow it to once more meet the circle at point D.

Seven Circle Theorem 1
\[{\bf{\triangle OAC}}\] and \[{\bf{\triangle OBC}}\], two triangles, are constructed. As a result, we note the following.
\[\angle {\bf{OAC}}{\rm{ }} = {\rm{ }}\angle {\bf{OCA}}\] in \[{\bf{\triangle OAC}}\] because \[{\bf{OA}}{\rm{ }} = {\rm{ }}{\bf{OC}}\]...( radii of the circle )
Because \[{\bf{OB}}{\rm{ }} = {\rm{ }}{\bf{OC}}\], in \[{\bf{\triangle OBC}}\], $\angle OBC =\angle OCB$ …(radii of the circle)
In triangle COB,
$\angle DOB = \angle OCB + \angle OBC$ (Exterior Angles)…(1)
In triangle COB,
OC = OB (Radius)
Thus, triangle COB is an isosceles triangle.
Therefore,
$\angle OCB = \angle OCB$ ...(2)
From equations (1) and (2),
$\angle DOB= 2\angle OCB$ …(3)
Similarly,
$\angle AOD = 2\angle ACO$...(4)
Equations (3) and (4) combined:
\[\begin{array}{*{20}{l}}{\angle AOD + {\rm{ }}\angle DOB = {\rm{ }}2 \times {\rm{ }}\left( {\angle ACO + {\rm{ }}\angle OCB} \right)}\\{ \Rightarrow {\rm{ }}\angle AOB = {\rm{ }}2 \times {\rm{ }}\angle ACB}\end{array}\]
Hence Proved.
Theorem 2: The diameter at the circumference forms a right angle with the surrounding plane.
Proof: Take a look at the illustration below, where AB represents the circle's diameter. We must demonstrate that $\angle ACB = 90^\circ$ .

Angle in a Semicircle
\[\angle {\bf{AOB}} = {\rm{ }}{\bf{2}} \times {\rm{ }}\angle {\bf{ACB}}\] is the result of applying Theorem 1: "The angle subtended by a chord at the centre is twice that subtended by it at the circumference." As AB is a straight line (diameter), \[\angle {\bf{AOB}}{\rm{ }} = {\rm{ }}{\bf{180}}^\circ \]. Inferring that\[\angle {\bf{ACB}}{\rm{ }} = {\rm{ }}{\bf{90}}^\circ ,{\rm{ }}{\bf{2}}{\rm{ }} \times {\rm{ }}\angle {\bf{ACB}}{\rm{ }} = {\rm{ }}{\bf{180}}^\circ \].
Hence Proved.
Theorem 3: The angles that the same arc subtends at its circumference are equal.
Proof: Take a look at the illustration below, which depicts an arc AB subtending angles ACB and ADB at two arbitrary places on the circle, C and D. The circle's centre is O.

Angles in The Same Segment of The Circle
We must demonstrate that \[\angle {\bf{ACB}} = {\rm{ }}\angle {\bf{ADB}}\].
The angle a chord subtends at the centre of a circle is twice as large as the angle it subtends at the circumference, according to the circle theorem.
\[\begin{array}{*{20}{l}}{\angle ACB = {\rm{ }}1/2 \times {\rm{ }}\angle AOB{\rm{ }} \cdots {\rm{ }}\left( 1 \right)}\\{\angle ADB = {\rm{ }}1/2 \times {\rm{ }}\angle AOB{\rm{ }} \cdots {\rm{ }}\left( 2 \right)}\end{array}\]
Equation (1) and equation (2) give us \[\angle {\bf{ACB}} = {\rm{ }}\angle {\bf{ADB}}\]. Since angles ACB and ADB are arbitrary angles, the conclusion holds for all angles that the same arc subtends.
Hence Proved.
Solved Examples
1. Consider a circle with the centre O. Utilising circle theorems, determine the value of x.

A Circle
Ans: A circle with the centre O is supplied, and since the radii OS and OT are equal, OS = OT. OTP = 90° is obtained by using the circle theorem, which states that the angle between the radius and the tangent at the point of contact is 90 degrees. Using the angle sum theorem and the triangle OTP, we have
$\begin{array}{*{20}{l}}{\angle TOP{\rm{ }} + {\rm{ }}\angle OTP{\rm{ }} + {\rm{ }}\angle OPT{\rm{ }} = {\rm{ }}180^\circ }\\{ \Rightarrow {\rm{ }}\angle TOP{\rm{ }} + {\rm{ }}90^\circ {\rm{ }} + {\rm{ }}32^\circ {\rm{ }} = {\rm{ }}180^\circ }\\{ \Rightarrow {\rm{ }}\angle TOP{\rm{ }} = {\rm{ }}180^\circ {\rm{ }} - {\rm{ }}\left( {90^\circ {\rm{ }} + {\rm{ }}32^\circ } \right)}\\{ = {\rm{ }}58^\circ }\end{array}$
Since
\[\begin{array}{l}OS{\rm{ }} = {\rm{ }}OT{\rm{ }}\\ \Rightarrow {\rm{ }}\angle OST{\rm{ }} = {\rm{ }}\angle OTS{\rm{ }} = {\rm{ }}x\end{array}\]
By the exterior angle theorem,
\[\begin{array}{*{20}{l}}{\angle OST{\rm{ }} + {\rm{ }}\angle OTS{\rm{ }} = {\rm{ }}\angle TOP}\\{ \Rightarrow {\rm{ }}x{\rm{ }} + {\rm{ }}x{\rm{ }} = {\rm{ }}58^\circ }\\{ \Rightarrow {\rm{ }}2x{\rm{ }} = {\rm{ }}58^\circ }\\{ \Rightarrow {\rm{ }}x{\rm{ }} = {\rm{ }}29^\circ }\end{array}\]
2. Assume the circle with O as the centre is shown below. Using the circle theorems, determine the value of POR.
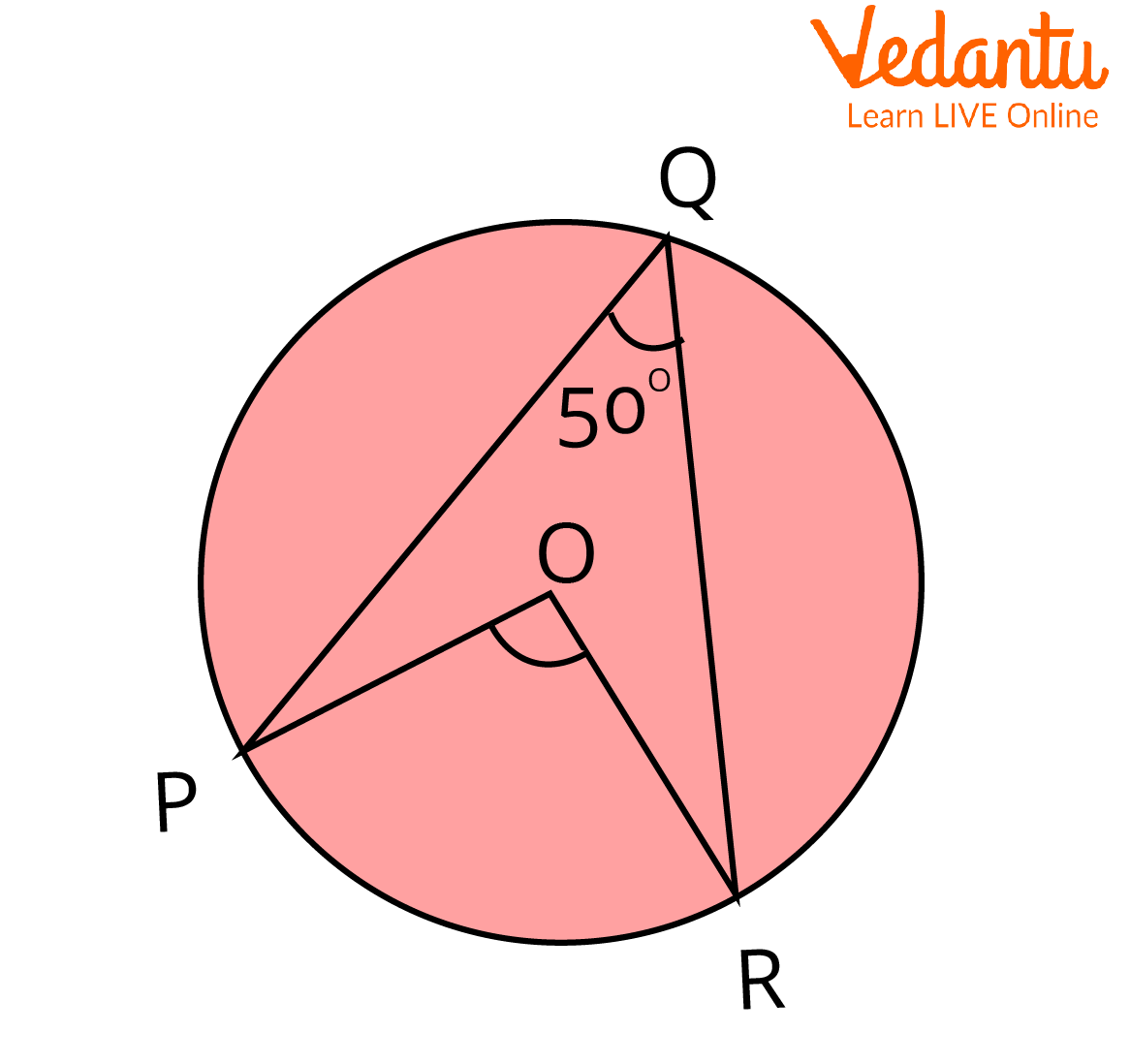
A Circle with Centre O
Ans: The circle theorem, which states that a chord's angle at the centre is twice that at the perimeter, will be used to determine the value of angle POR. Thus, \[\angle POR{\rm{ }} = {\rm{ }}2\angle PQR\].
Given that \[\angle PQR{\rm{ }} = {\rm{ }}50^\circ \], we have
\[\begin{array}{*{20}{l}}{\angle POR{\rm{ }} = {\rm{ }}2\angle PQR}\\{ \Rightarrow {\angle POR = {\rm{ }}2{\rm{ }} \times {\rm{ }}50^\circ }}\\{\angle POR= {\rm{ }}100^\circ }\end{array}\]
3. Consider the circle with O as the centre is shown below. Using the circle theorems, determine the angle x.

Unknown Angle x
Ans: The angle subtended by the diameter at the circumference is a right angle, according to the circle theorem, hence \[\angle ABC{\rm{ }} = {\rm{ }}90^\circ \]. The triangular sum theorem demonstrates that\[\angle BAC{\rm{ }} + {\rm{ }}\angle ACB{\rm{ }} + {\rm{ }}\angle ABC{\rm{ }} = {\rm{ }}180^\circ \].
\[\begin{array}{*{20}{l}}{ \Rightarrow {\rm{ }}x{\rm{ }} + {\rm{ }}55^\circ {\rm{ }} + {\rm{ }}90^\circ {\rm{ }} = {\rm{ }}180^\circ }\\{ \Rightarrow {\rm{ }}x{\rm{ }} + {\rm{ }}145^\circ {\rm{ }} = {\rm{ }}180^\circ }\\{ \Rightarrow {\rm{ }}x{\rm{ }} = {\rm{ }}180^\circ {\rm{ }} - {\rm{ }}145^\circ }\\{ = {\rm{ }}35^\circ }\end{array}\]
Applications of the Seven Circle Theorems
Circle theorems are required to address a variety of geometric issues. When we draw angles and lines inside of a circle, we can infer several patterns and theorems that are useful in both theoretical and practical contexts.
Important Points to Remember
Geometric theorems about circles are essential conclusions that can be utilised to answer a variety of geometrical problems.
Angles subtended by the same arc at the circumference are equal.
Conclusion
The article went into detail about circles. The topic of the seven circle theorems is discussed. Each of the seven has a unique place in Mathematics. Geometrical circle theorems pertain to the several parts of a circle, such as a chord, segments, sector, diameter, tangent, etc.
FAQs on Seven Circle Theorems: Concepts, Proofs & Applications
1. What are the essential circle theorems for CBSE Classes 9 and 10?
The core circle theorems in the CBSE syllabus provide foundational rules about angles, chords, and tangents. The main theorems include:
- The angle at the centre is double the angle at the circumference subtended by the same arc.
- Angles in the same segment of a circle are equal.
- The sum of opposite angles in a cyclic quadrilateral is 180°.
- The radius is perpendicular to the tangent at the point of contact.
- The lengths of two tangents drawn from an external point to a circle are equal.
2. What does it mean for an arc to 'subtend' an angle in a circle?
In geometry, to 'subtend' means to create or form an angle at a specific point. When we say an arc subtends an angle, it means that lines are drawn from the two endpoints of the arc to meet at a point. This point could be the centre of the circle (forming the central angle) or any point on the remaining part of the circumference (forming an inscribed angle).
3. How is the angle at the centre related to the angle at the circumference subtended by the same arc?
The relationship is a fundamental theorem: the angle that an arc of a circle subtends at the centre is exactly double the angle it subtends at any point on the remaining part of the circle. For instance, if an arc creates a 140° angle at the centre, the angle it subtends at the circumference will be 70°.
4. Why are angles formed in the same segment of a circle always equal?
This is a direct consequence of the centre-angle theorem. All angles in the same segment are subtended by the same arc on the opposite side of the circle. Since each of these angles is exactly half the angle subtended by this common arc at the centre, they must all be equal to each other. The central angle acts as a constant reference for them.
5. What is the difference between a tangent and a secant to a circle?
The key difference lies in the number of points they touch the circle:
- A tangent is a line that intersects the circle at exactly one point. This point is called the point of tangency or point of contact.
- A secant is a line that intersects the circle at two distinct points, effectively passing through the interior of the circle.
6. What is the key property of opposite angles in a cyclic quadrilateral?
The most important property of a cyclic quadrilateral (a four-sided figure with all its vertices on a circle's circumference) is that its opposite angles are supplementary. This means that the sum of each pair of opposite angles is exactly 180°. For example, in a cyclic quadrilateral ABCD, ∠A + ∠C = 180° and ∠B + ∠D = 180°.
7. If a quadrilateral has one pair of opposite angles that sum to 180°, can it always be considered cyclic?
Yes, absolutely. This is the converse of the cyclic quadrilateral theorem. If you can prove that just one pair of opposite angles in a quadrilateral adds up to 180°, it is sufficient to prove that the quadrilateral is cyclic. This means a circle can be drawn passing through all four of its vertices.
8. How are circle theorems applied in real-world scenarios like engineering or architecture?
Circle theorems are not just theoretical concepts; they are crucial in practical applications. For example:
- Architecture: Architects use theorems to design curved structures like domes, arches, and stained-glass windows, ensuring stability and correct angle placement.
- Engineering: Engineers apply these principles in designing gears, wheels, and bearings, where the relationships between tangents and radii are critical for smooth operation.
- Navigation and GPS: Satellite and ship navigation use triangulation principles that rely on the geometric properties of circles and angles to pinpoint locations.




























