Tangent Segment Theorem Explained for Students

A tangent is a line drawn from a point on the circle connecting two points that are infinitely close to one another. In other words, we might state that Tangents are the lines that precisely cross the circles at a single point. The tangent's point of tangency is where it touches the circle. The radius is perpendicular to a tangent at the point of tangency. Due to its importance in geometrical constructions and proofs, it is related to numerous theorems.

Tangent to a Circle

What is the Tangent Segment Theorem?

According to the Tangent Segment Theorem, two tangent segments from an exterior point to a circle are congruent. The line connecting the exterior point and the point of tangency is referred to as a tangent segment.

In simple words, we can say that the tangent segments traced from an external point (point outside the circle) to the circle are congruent.

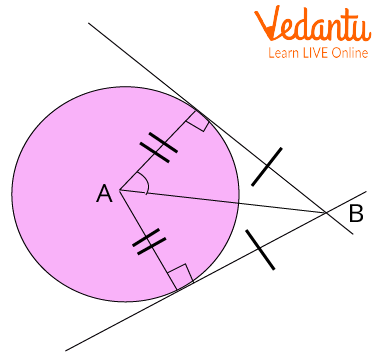
Tangent Segments Traced from An External Point to The Circle

Tangent Segment Theorem Proof

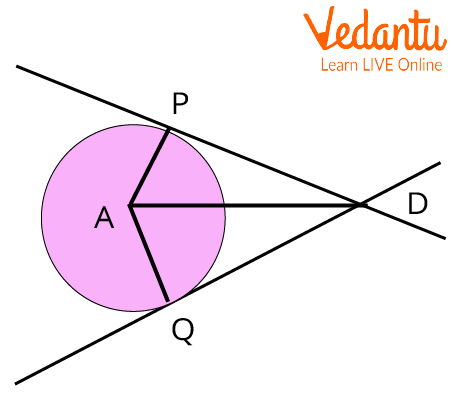
Tangent Segment Theorem Proof

Let A be the centre of the circle and the line DP and line DQ are the tangents to the circle at points P and Q, respectively. And we need to prove that the segment DP is congruent to segment DQ. So let’s draw a segment AD and radii AP and AQ. By the Tangent theorem, we know that the tangent at any point of the circle is perpendicular to the radius through the point of contact.

In $\triangle PAD$ and $\triangle QAD$,

$Seg AP \cong Seg AQ $ …(Radii of the same circle)

$Seg AD \cong Seg AD$ …(Common Side)

By the Tangent theorem,

$\angle APD = \angle AQD = 90^{\circ}$

And

$\triangle PAD \cong \triangle QAD$ …(Hypotenuse- Side Test)

Therefore, by CPCT,

$Seg DP \cong Seg DQ$

Hence Proved.

Applications of Tangents Segment Theorem

• The tangent segment theorem can be applied to calculate the various angles that the tangents make.

• Two tangent segments from an outside point to a circle can be shown to be identical by using the tangent segment theorem.

Tangent Segment Theorem Examples

1. In the figure given below, a circle with centre D touches the sides of $\angle ACB$ at A and B. If $\angle ACB$ is $52^\circ $, find the measure of $\angle ADB$.

A Circle and Two Tangent Lines

Ans: As known, the sum of all the angles of a quadrilateral is $360^\circ $.

And by Tangent theorem,

$\angle CAD\; = \;\angle CBD\; = \;90^\circ $

Therefore,

$\begin{array}{l}\angle ACB + \angle CAD\; + \angle CBD + \angle ADB\; = \;360^\circ \\ \Rightarrow 52^\circ + 90^\circ + 90^\circ + \angle ADB\; = \;360^\circ \\ \Rightarrow 232^\circ + \angle ADB\; = \;360^\circ \\ \Rightarrow \angle ADB\; = \;360^\circ \; - \;232^\circ \; = 128^\circ \\\angle ADB\; = \;128^\circ \end{array}$

2. Demonstrate that $AB = AC$ if AB and AC are tangent to circle O.

Ans: Let’s first draw a figure according to the given situation.

Equal Tangents

Now, we know

AB and AC are tangents to Circle O (Given).

The tangent lines are perpendicular to the radius of the circle. So,

$\angle ABO = \angle ACO = 90^\circ \;\;\;$

By reflexive property,

$AO = AO$(Common Sides)

As the radii of the circle are all equal.

So,

$OC\; = \;OB\; = \;r$

Therefore, $\vartriangle ABO\cong \vartriangle ACO~~$(Hypotenuse-leg )

Therefore, by CPCTC,

$AB = AC$

Hence Proved.

3. An exterior point T leads two tangents, TP and TQ, to a circle with the centre O. Prove that $\angle PTQ\; = \;2\angle OPQ$

Ans: Let’s first draw a figure according to the given situation.

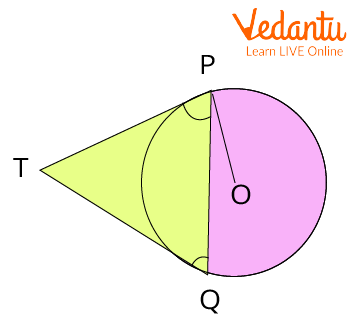
Tangent Segment Theorem

By the Tangent Segment theorem,

$TP = TQ$

$\therefore \angle TQP = \angle TPQ$

Now,

OP is the radius of the circle and PT is the tangent, therefore,

$OP \bot TP$

So,

$\angle OPT = 90^\circ $

$ \Rightarrow \angle OPQ + \angle TPQ = 90^\circ $

$ \Rightarrow \angle TPQ = 90^\circ - \angle OPQ \cdots \left( 1 \right)$

In $\triangle PTQ$,

$\angle TPQ + \angle TQP + \angle PTQ = 180^{\circ}$

$ \Rightarrow 2\angle TPQ + \angle PTQ = 180^{\circ}$ (because $ \angle TPQ = \angle TQP$)

$ \Rightarrow 2(90^{\circ} - \angle OPQ )+ \angle PTQ = 180^{\circ}$ ( from (1)) $\Rightarrow 180^{\circ} - 2\angle OPQ + \angle PTQ = 180^{\circ}$

$ \Rightarrow \angle PTQ = 2\angle OPQ$

Hence Proved.

Important Points to Remember

• A circle's tangent segments which are drawn from a point outside the circle are congruent.

• Tangent segments to the circle form congruent angles with the line joining the point to the circle's centre when released from a point outside the circle.

Important Formula from the Theorem

According to the tangent segment theorem, if tangents are drawn from an external point(P) of a circle with centre O, then both tangents at point Q and R are congruent,

PQ = PR.

Conclusion

In this article, we have thoroughly discussed the tangent segment theorem and its proof. From the discussion above about the tangent segment theorem, we can conclude that two tangent segments from an exterior point to a circle are congruent.