NCERT Solutions for Class 9 Maths Chapter 1 Number System Ex 1.4

Exercise 1.4

1. Classify the Following Numbers As Rational or Irrational:

(i) $ {2-}\sqrt{ {5}}$

Ans: The given number is $2-\sqrt{5}$.

Here, $\sqrt{5}=2.236.....$ and it is a non-repeating and non-terminating irrational number.

Therefore, substituting the value of $\sqrt{5}$ gives

$2-\sqrt{5}=2-2.236.....$

$=-0.236.....$, which is an irrational number.

So, $2-\sqrt{5}$ is an irrational number.

(ii) $\left(  {3+}\sqrt{ {23}} \right) {-}\left( \sqrt{ {23}} \right)$

Ans: The given number is $\left( 3+\sqrt{23} \right)-\left( \sqrt{23} \right)$.

The number can be written as

\begin{align} & \left( 3+\sqrt{23} \right)-\sqrt{23}=3+\sqrt{23}-\sqrt{23} \\ & =3 \end{align}

$=\dfrac{3}{1}$, which is in the $\dfrac{p}{q}$ form and so, it is a rational number.

Hence, the number $\left( 3+\sqrt{23} \right)-\sqrt{23}$ is a rational number.

(iii) $\dfrac{ {2}\sqrt{ {7}}}{ {7}\sqrt{ {7}}}$

Ans: The given number is $\dfrac{2\sqrt{7}}{7\sqrt{7}}$.

The number can be written as

$\dfrac{2\sqrt{7}}{7\sqrt{7}}=\dfrac{2}{7}$, which is in the $\dfrac{p}{q}$  form and so, it is a rational number.

Hence, the number  $\dfrac{2\sqrt{7}}{7\sqrt{7}}$ is a rational number.

(iv) $\dfrac{ {1}}{\sqrt{ {2}}}$

Ans: The given number is $\dfrac{1}{\sqrt{2}}$.

It is known that, $\sqrt{2}=1.414.....$ and it is a non-repeating and non-terminating irrational number.

Hence, the number $\dfrac{1}{\sqrt{2}}$ is an irrational number.

(v) $ {2\pi }$

Ans: The given number is $2\pi $.

It is known that, $\pi =3.1415$ and it is an irrational number.

Now remember that, Rational $\times $ Irrational = Irrational.

Hence, $2\pi $ is also an irrational number.

2. Simplify Each of the of the Following Expressions:

(i) $\left(  {3+}\sqrt{ {3}} \right)\left(  {2+}\sqrt{ {2}} \right)$

Ans: The given number is $\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)$.

By calculating the multiplication, it can be written as

$\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)=3\left( 2+\sqrt{2} \right)+\sqrt{3}\left( 2+\sqrt{2} \right)$.

$=6+3\sqrt{2}+2\sqrt{3}+\sqrt{6}$.

(ii) $\left(  {3+}\sqrt{ {3}} \right)\left(  {3-}\sqrt{ {3}} \right)$

Ans: The given number is $\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)$.

By applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, the number can be written as

$\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)={{3}^{2}}-{{\left( \sqrt{3} \right)}^{2}}=9-3=6$.

(iii)  ${{\left( \sqrt{ {5}} {+}\sqrt{ {2}} \right)}^{ {2}}}$

Ans: The given number is ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$.

Applying the formula ${{\left( a+b \right)}^{2}}={{a}^{2+}}2ab+{{b}^{2}}$, the number can be written as

${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+2\sqrt{5}\sqrt{2}+{{\left( \sqrt{2} \right)}^{2}}$

$=5+2\sqrt{10}+2$

$=7+2\sqrt{10}$.

(iv)  $\left( \sqrt{ {5}}-\sqrt{ {2}} \right)\left( \sqrt{ {5}} {+}\sqrt{ {2}} \right)$

Ans: The given number is $\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)$.

Applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, the number can be expressed as

$\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)={{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}$

=5 - 2

= 3

3. Recall that, $ {\pi }$ is defined as the ratio of the circumference (say $ {c}$) of a circle to its diameter (say $ {d}$). That is, $ {\pi =}\dfrac{ {c}}{ {d}}$ .This seems to contradict the fact that $ {\pi }$ is irrational. How will you resolve this contradiction?

Ans: It is known that, $\pi =\dfrac{22}{7}$, which is a rational number. But, note that this value of $\pi $ is an approximation.

On dividing $22$ by $7$, the quotient $3.14...$ is a non-recurring and non-terminating number. Therefore, it is an irrational number.

In order of increasing accuracy, approximate fractions are

$\dfrac{22}{7}$, $\dfrac{333}{106}$, $\dfrac{355}{113}$, $\dfrac{52163}{16604}$, $\dfrac{103993}{33102}$, and \[\dfrac{245850922}{78256779}\].

Each of the above quotients has the value $3.14...$, which is a non-recurring and non-terminating number.

Thus, $\pi $ is irrational.

So, either circumference $\left( c \right)$ or diameter $\left( d \right)$ or both should be irrational numbers.

Hence, it is concluded that there is no contradiction regarding the value of $\pi $ and it is made out that the value of $\pi $ is irrational.

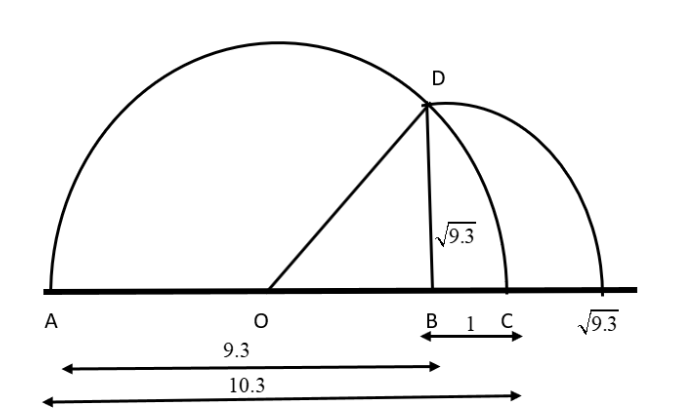
4. Represent $\sqrt{ {9} {.3}}$ on the number line.

Ans: Follow the procedure given below to represent the number $\sqrt{9.3}$.

• First, mark the distance $9.3$ units from a fixed-point $A$ on the number line to get a point $B$. Then $AB=9.3$ units.

• Secondly, from the point $B$ mark a distance of $1$ unit and denote the ending point as $C$.

• Thirdly, locate the midpoint of $AC$ and denote as $O$.

• Fourthly, draw a semi-circle to the centre $O$ with the radius $OC=5.15$ units. Then 

$\begin{align}& AC=AB+BC \\& =9.3+1 \\& =10.3 \\\end{align}$ 

So, $OC=\dfrac{AC}{2}=\dfrac{10.3}{2}=5.15$.

• Finally, draw a perpendicular line at $B$ and draw an arc to the centre $B$ and then let it meet at the semicircle $AC$ at $D$ as given in the diagram below.

5. Rationalize the denominators of the following:

(i) $\dfrac{ {1}}{\sqrt{ {7}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}}$.

Multiplying and dividing by $\sqrt{7}$ to the number gives

$\dfrac{1}{\sqrt{7}}\times \dfrac{\sqrt{7}}{\sqrt{7}}=\dfrac{\sqrt{7}}{7}$.

(ii) $\dfrac{ {1}}{\sqrt{ {7}} {-}\sqrt{ {6}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}-\sqrt{6}}$.

Multiplying and dividing by $\sqrt{7}+\sqrt{6}$ to the number gives

$\dfrac{1}{\sqrt{7}-\sqrt{6}}\times \dfrac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}=\dfrac{\sqrt{7}+\sqrt{6}}{\left( \sqrt{7}-\sqrt{6} \right)\left( \sqrt{7}+\sqrt{6} \right)}$

Now, applying the formula $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$ to the denominator gives

$\begin{align} & \dfrac{1}{\sqrt{7}-\sqrt{6}}=\dfrac{\sqrt{7}+\sqrt{6}}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( \sqrt{6} \right)}^{2}}} \\ & =\dfrac{\sqrt{7}+\sqrt{6}}{7-6} \\& =\dfrac{\sqrt{7}+\sqrt{6}}{1}. \\ \end{align}$

(iii) $\dfrac{ {1}}{\sqrt{ {5}} {+}\sqrt{ {2}}}$

Ans: The given number is $\dfrac{1}{\sqrt{5}+\sqrt{2}}$.

Multiplying and dividing by $\sqrt{5}-\sqrt{2}$ to the number gives

$\dfrac{1}{\sqrt{5}+\sqrt{2}}\times \dfrac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}=\dfrac{\sqrt{5}-\sqrt{2}}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)}$

Now, applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$  to the denominator gives

$\begin{align}&\dfrac{1}{\sqrt{5}+\sqrt{2}}=\dfrac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5}\right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}} \\ & =\dfrac{\sqrt{5}-\sqrt{2}}{5-2}\\& =\dfrac{\sqrt{5}-\sqrt{2}}{3}. \\\end{align}$

(iv) $\dfrac{ {1}}{\sqrt{ {7}} {-2}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}-2}$.

Multiplying and dividing by $\sqrt{7}+2$ to the number gives

$\dfrac{1}{\sqrt{7}-2}=\dfrac{\sqrt{7}+2}{\left( \sqrt{7}-2 \right)\left( \sqrt{7}+2 \right)}\\$.

Now, applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ to the denominator gives

$\begin{align}& \dfrac{1}{\sqrt{7}-2}=\dfrac{\sqrt{7}+2}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( 2 \right)}^{2}}}\\& =\dfrac{\sqrt{7}+2}{7-4}\\& =\dfrac{\sqrt{7}+2}{3}. \\\end{align}$

Conclusion

This Class 9 Maths Chapter 1 Exercise 1.4 reinforces your grasp of rational and irrational numbers. You've honed your ability to classify them based on their decimal representations and investigated how basic mathematical operations (addition, subtraction, multiplication, and division) affect these categories. Remember, rational numbers can always be written as fractions, whereas irrational numbers have never-ending, non-repeating decimal expansions. Having a solid foundation in these concepts will prove valuable as you delve into more intricate problems involving real numbers in the chapters ahead. Solving Class 9 Maths Ch 1 Ex 1.4 will give students a boost to score good marks in their exams.

Class 9 Maths Chapter 1: Exercises Breakdown

CBSE Class 9 Maths Chapter 1 Other Study Materials

Chapter-Specific NCERT Solutions for Class 9 Maths

Given below are the chapter-wise NCERT Solutions for Class 9 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Study Materials for CBSE Class 9 Maths