A clock was set correct at 12 o’clock. It loses 10 minutes per hour. What will be the angle between the hour and the minute hand of the clock after one hour?
A. ${{60}^{\circ }}$
B. ${{90}^{\circ }}$
C. ${{105}^{\circ }}$
D. ${{75}^{\circ }}$

Hint: In this question we have been given that the clock loses 10 minutes per hour and we have to find the angle between the hour hand and the minute hand of the clock after 1 hour. From the given data, we will conclude that it will show 50 minutes for the next 60 minutes and hence the time will be 12:50 instead of 1 o’clock. After that, we will find the angle covered by the minute hand in 1 hour and then subtract it from ${{360}^{\circ }}$. This will give us our required angle.

Complete step-by-step answer:
Now, we have been given that the clock loses 10 minutes per hour. This means that the minute hand will move for $60-10=50$ minutes in one hour instead of 60 minutes and then $50-10=40$ minutes in the next hour and so on.
Thus, after 1 hour, the minute hand will show 50 minutes. So the time will be 12:50 instead of 1 o’clock.
Thus, the clock will look some like this:

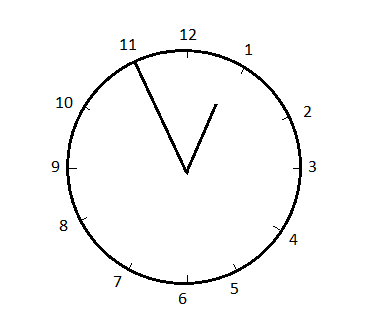
So, in 1 hour, the angle covered by the minute hand is given as:
$\begin{align}
  & \dfrac{50}{60}\times {{360}^{\circ }} \\
 & \Rightarrow {{300}^{\circ }} \\
\end{align}$
Thus, the angle between the minute hand and the hour hand will be ${{360}^{\circ }}$ minus the angle covered by the minute hand in 1 hour.
Thus, the required angle is given as:
$\begin{align}
  & {{360}^{\circ }}-{{300}^{\circ }} \\
 & \Rightarrow {{60}^{\circ }} \\
\end{align}$
Thus, the required angle is ${{60}^{\circ }}$

So, the correct answer is “Option A”.

Note: To find out the angle swept by the minute hand in ‘x’ minutes, we use the formula:
$\theta =\dfrac{x}{60}\times {{360}^{\circ }}$
This is derived as:
We know that in one hour there are 60 minutes and the minute hand in the clock completes one revolution in that time.
Thus the angle swept by the minute hand in 1 hour is:
$\dfrac{{{360}^{\circ }}}{60}$
Thus, the angle swept by the minute hand is given as:
$\begin{align}
  & x\times \dfrac{{{360}^{\circ }}}{60} \\
 & \Rightarrow \dfrac{x}{60}\times {{360}^{\circ }} \\
\end{align}$