A ray is incident at an angle of incidence i on one surface of a prism of small angle A and emerges normally from the opposite direction. If the refractive surface of the material of the prism is $\mu $, the angle of the incidence i is nearly equal to:
$
  (a){\text{ }}\dfrac{{\mu A}}{2} \\
  (b){\text{ }}\dfrac{A}{{2\mu }} \\
  (c){\text{ }}\mu {\text{A}} \\
  {\text{(d) }}\dfrac{A}{\mu } \\
 $

Hint: In this question use the concept that since incident ray emerges normally from the opposite surface of the prism so the angle of emergence becomes zero that is $\angle e = 0$. Then use the fact that in a prism, small angle of prism plus angle of deviation in a prism is equal to the sum of angle of incidence and angle of emergence that is $\delta + A = i + e$ along with the relation between angle of deviation ($\delta $), small angle of prism (A) and the refractive index of the prism ($\mu $) that is $\delta = \left( {\mu - 1} \right)A$. This will help approach the solution of this problem.

Complete step-by-step solution:


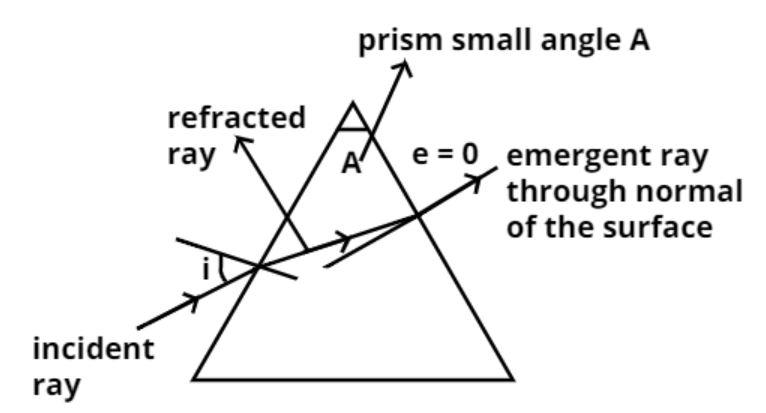
Given data:
Angle of incident = i
Prism small angle = A
Refractive material of the prism = $\mu $
Let the angle of emergence = e
Now it is given that the incident ray emerges normally from the opposite surface of the prism so the angle of emergence becomes zero.
$ \Rightarrow \angle e = 0$................... (1)
Let angle of deviation in the prime be $\delta $
So as we know the relation between angle of deviation ($\delta $), small angle of prism (A) and the refractive index of the prism ($\mu $) which is given as,
$ \Rightarrow \delta = \left( {\mu - 1} \right)A$................... (2)
Now as we know in a prism, a small angle of prism plus angle of deviation in a prism is equal to the sum of angle of incidence and angle of emergence.
Therefore, we have,
$ \Rightarrow \delta + A = i + e$................ (3)
Now substitute the value from equation (1) and (2) in equation (3) we have,
$ \Rightarrow \left( {\mu - 1} \right)A + A = i + 0$
Now simplify the above equation we have,
$ \Rightarrow \mu A - A + A = i$
Now cancel out the positive, negative same terms we have,
$ \Rightarrow i = \mu A$
So this is the required angle of incidence such that the prism has small angle A and emerges normally from the opposite surface.
So this is the required answer.
Hence option (C) is the correct answer.

Note – It is important to understand the concept of angle of prism as any angle inside a prism can’t be considered as the angle of the prism. So angle of prism is specifically defined as the angle between those two surfaces of the prism one from which the light enters the prism and the one from which the light goes out of the prism after the refraction.