An asteroid is moving directly towards the centre of the earth. When at a distance of $10$R (R is the radius of the earth) from the earth centre, it has a speed of $12$km/s. Neglecting the effect on the earth's atmosphere, what will be the speed of the asteroid when it hits the surface of the earth (escape velocity from the earth is $11.2$km/s)? Give your answer to the nearest integer in Kilometre/s_ _ _ _ _ _

Hint: As the asteroid is moving towards earth, then by conservation by mechanical energy, the total energy at a distance $10R$ from the centre of earth will be the same as the total energy at distance R from the centre of earth.
Formula used:
1. Initial Mechanical Energy $ = $ Final Mechanical Energy
2. $K.E = \dfrac{1}{2}m{v^2}$
3. Potential Energy $ = \dfrac{{ - GMm}}{R}$

Complete step by step answer:
Let the velocity of asteroid at distance $10R$ from centre of Earth by, $u = 12km/s$ and the final velocity of asteroid at a distance R from the centre of earth be v km/s as shown in figure below:





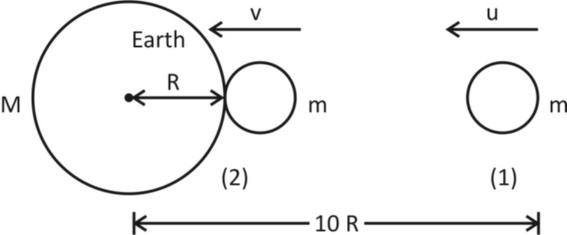
Now, initial Mechanical Energy $ = $ Initial kinetic energy $ + $ initial potential energy
$ = \dfrac{1}{2}m{u^2} + \left( {\dfrac{{ - GMm}}{{10R}}} \right)$
And Final Mechanical energy $ = $ Final kinetic energy $ + $ initial potential energy
$ = \dfrac{1}{2}m{u^2} + \left( {\dfrac{{ - GMm}}{{10R}}} \right)$
Where M is mass of Earth
m is mass of asteroid
R is radius of earth and
G is universal Gravitational constant
So, by conservation of mechanical energy, initial mechanical energy $ = $ final mechanical energy
$ \Rightarrow \dfrac{1}{2}m{u^2} + \left( {\dfrac{{ - GMm}}{{10R}}} \right) = \dfrac{1}{2}m{v^2} + \left( {\dfrac{{ - GMm}}{R}} \right)$
$ \Rightarrow \dfrac{1}{2}m{v^2} - \dfrac{1}{2}m{u^2} = \dfrac{{ - GMm}}{{10R}} + \dfrac{{ - GMm}}{R}$
$ \Rightarrow \dfrac{1}{2}\left( {{v^2} - {u^2}} \right) = \dfrac{{ - GMm}}{R}\left( {\dfrac{1}{{10}} - 1} \right)$
$ \Rightarrow \dfrac{1}{2}\left( {{v^2} - {u^2}} \right) = \dfrac{{ - GM}}{R} \times \dfrac{{ - 9}}{{10}}$
$ \Rightarrow {v^2} - {u^2} = \dfrac{{9GM}}{{10R}} \times 2$
$ \Rightarrow {v^2} = {u^2} + \dfrac{{9GM}}{{5R}}........\left( 1 \right)$
Now, here $u = 12km/s = 12000m/s$
M$ = $ mass of earth
As $\dfrac{{GM}}{{{R^2}}} = g \Rightarrow \dfrac{{GM}}{R} = gR$
So, \[{v^2} = {u^2} + \dfrac{9}{5}gR\]
\[\Rightarrow {v^2} = {\left( {12000} \right)^2} + \dfrac{9}{5} \times 9.8 \times 6400000\]
\[\Rightarrow {v^2} = 14000000 + 112896000\]
\[\Rightarrow {v^2} = 256,896,000\]
\[\Rightarrow v = 16,027.97m/s\]
$\Rightarrow v \simeq 16km/s$

Note:
The relation between acceleration due to gravity, g and universal gravitational constant, G is
$g = \dfrac{{GM}}{{{R^2}}} \Rightarrow \dfrac{{GM}}{R} = gR$
So, we have replaced $\dfrac{{GM}}{R}$ with gR in equation ....(1).