An example for a function which is a relation, (Domain-R, Codomain-R) is:
This question has multiple correct options
A. $y = x$
B. $y = x - 1$
C. $y = {x^2}$
D. None of these

Hint- Here, we will proceed by analysing the graph of each function and then drawing a vertical line.
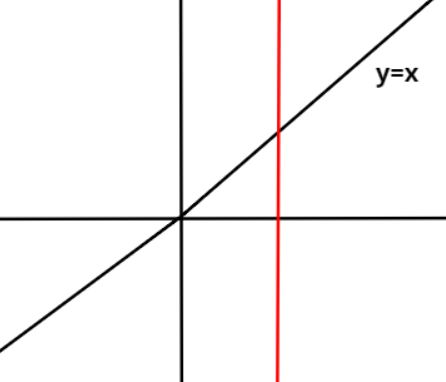
Every function is a relation when each input has only one output. It means that for a particular value of $x$, there should be only one value of $y$ corresponding to that value of $x$.
This can be checked by drawing a vertical line in the graph of the function and if this vertical line cuts at exactly one point on the curve of the function, then that function is a relation whereas if this vertical line cuts at more than one point on the curve of the function, then this function is not a relation.
Now, figures corresponding to each function given in the options are drawn and then a vertical line is also drawn in each figure. Clearly, in all the figures the vertical line is cutting at exactly one point. Thereby, showing that for one input value there is only one output value.
Hence, all the three given functions i.e., $y = x$, $y = x - 1$ and $y = {x^2}$are examples of relations.
Therefore, options A, B and C are correct.

Note- For function $y = {x^2}$, at $x = 1$ and $x = - 1$ the value of the function is the same which is $y = 1$. Here, corresponding to two inputs there is one same value of output which is possible for a relation because corresponding to each value of input there is only one output.