How can the distance formula be used in real life?

Hint: We will first learn about the distance formula, that is how we use it to find distances. Then we will look for possible ways to use it in real life. We will learn about the various terms and the places where we can use the distance formula to get the distances and how it can be useful in real life.

Complete step-by-step solution:
We are asked about the practical application of the distance formula. We start the solution first by understanding what the distance formula is. In coordinate geometry, we use the distance formula to find the distance between two coordinates, which is given as,
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the coordinates of those two points.
The distance formula is derived using mathematician Pythagoras’s theorem, Pythagoras Theorem.

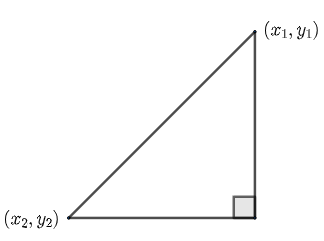
$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
It has various applications in daily life. It is used in navigation. The pilot of a plane calculates the distance between their plane and the other plane using the distance formula. They find the coordinate of the plane and then apply the distance formula to get the distance. We can consider another example. If we wish to find the length of the building whose coordinates of the foot and the top are given, then we can use the distance formula. The ship also uses the distance formula for navigation.

Note: In coordinate geometry, we use it to find the distance between any two coordinates. We use the same formula in 3-dimensional as $d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}+{{\left( {{z}_{1}}-{{z}_{2}} \right)}^{2}}}$. We also have other formulas in coordinate geometry like the section formula, which helps us to find the point that lies between the given two coordinates. The ship uses it to get the meeting point and adjust their speed so that the ships don’t collide on meeting too near to each other.