
Find the value of the given trigonometric ratio, $\tan 15{}^\circ $ .
Answer
552.9k+ views
Hint: Use the formula of $\tan 2A$ along with the value of $\tan 30{}^\circ $ , to get a quadratic equation. Solve the quadratic equation to reach the required answer.
Complete step-by-step answer:
We know;
$\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$
The other commonly used trigonometric values include:
$\tan 0{}^\circ =0$
$\tan 45{}^\circ =1$
$\tan 60{}^\circ =\sqrt{3}$
Also, we have, the formula: $\tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$
So, in the above formula substituting $A=15{}^\circ $ .
$\therefore \tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$
$\Rightarrow \tan \left( 2\times 15{}^\circ \right)=\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
$\Rightarrow \tan 30{}^\circ =\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
Putting the value of $\tan 30{}^\circ $ in the equation, we get;
$\dfrac{1}{\sqrt{3}}=\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
On cross-multiplication, we get;
$1-{{\tan }^{2}}15{}^\circ =2\sqrt{3}\tan 15{}^\circ $
$\Rightarrow {{\tan }^{2}}15{}^\circ +2\sqrt{3}\tan 15{}^\circ -1=0$
So, the equation we get is a quadratic equation, and one of the roots of this quadratic equation would be the value of $\tan 15{}^\circ $.
We know, for a quadratic equation of the form $a{{x}^{2}}+bx+c=0$ .
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Applying the formula to our quadratic equation, we have;
$\tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-4\times 1\times \left( -1 \right)}}{2\times 1}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{12+4}}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{16}}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm 4}{2}$
We know, $15{}^\circ $ lies in the first quadrant.
According to the graph of $\tan (x)$ :
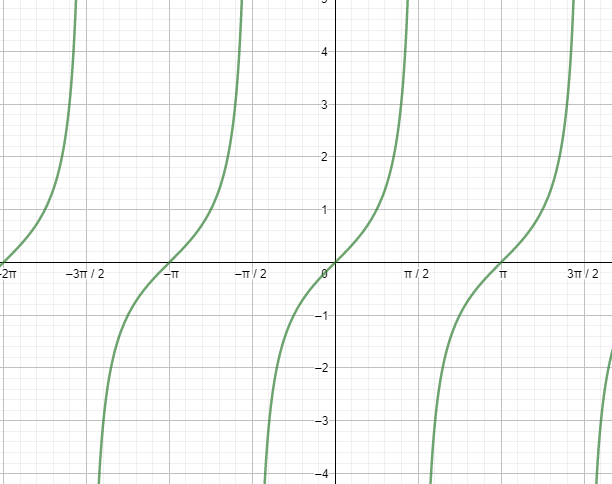
$\tan (x)$ is positive when x lies in the first quadrant.
Therefore, $\tan 15{}^\circ $ is also positive.
$\therefore \tan 15{}^\circ =\dfrac{-2\sqrt{3}+4}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{\left( -\sqrt{3}+2 \right)}{{}}$
$\therefore \tan 15{}^\circ =2-\sqrt{3}$
Hence, the value of $\tan 15{}^\circ $ is $2-\sqrt{3}$ .
Note: Other useful formulas include:
$\tan (A+B)=\dfrac{\tan A+\tan B}{1-\tan A\tan B}$
$\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$
And you are free to use any formula, just substitute the angles according to the need to get the desired values.
We can also find the value of $\tan 15{}^\circ $ using formula: $\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$ .
On Substituting A and B in the above formula, we get;
$A=45{}^\circ $
$B=30{}^\circ $
The equation becomes:
$\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$
$\Rightarrow \tan (45{}^\circ -30{}^\circ )=\dfrac{\tan 45{}^\circ -\tan 30{}^\circ }{1+\tan 45{}^\circ \tan 30{}^\circ }$
\[\Rightarrow \tan 15{}^\circ =\dfrac{1-\left( \dfrac{1}{\sqrt{3}} \right)}{1+1\times \dfrac{1}{\sqrt{3}}}\]
Point to remember: whenever you try to find the value of $\sin 15{}^\circ $ , don’t use the formula of $\sin 2A$ , instead, go for the formula: $\cos 2A=1-2{{\sin }^{2}}A$ . The reason being, whenever you use the formula of $\sin 2A$ , you get both $\cos A$ and $\sin A$ to be unknown, making it difficult to solve.
Complete step-by-step answer:
We know;
$\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$
The other commonly used trigonometric values include:
$\tan 0{}^\circ =0$
$\tan 45{}^\circ =1$
$\tan 60{}^\circ =\sqrt{3}$
Also, we have, the formula: $\tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$
So, in the above formula substituting $A=15{}^\circ $ .
$\therefore \tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$
$\Rightarrow \tan \left( 2\times 15{}^\circ \right)=\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
$\Rightarrow \tan 30{}^\circ =\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
Putting the value of $\tan 30{}^\circ $ in the equation, we get;
$\dfrac{1}{\sqrt{3}}=\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
On cross-multiplication, we get;
$1-{{\tan }^{2}}15{}^\circ =2\sqrt{3}\tan 15{}^\circ $
$\Rightarrow {{\tan }^{2}}15{}^\circ +2\sqrt{3}\tan 15{}^\circ -1=0$
So, the equation we get is a quadratic equation, and one of the roots of this quadratic equation would be the value of $\tan 15{}^\circ $.
We know, for a quadratic equation of the form $a{{x}^{2}}+bx+c=0$ .
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Applying the formula to our quadratic equation, we have;
$\tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-4\times 1\times \left( -1 \right)}}{2\times 1}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{12+4}}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{16}}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm 4}{2}$
We know, $15{}^\circ $ lies in the first quadrant.
According to the graph of $\tan (x)$ :

$\tan (x)$ is positive when x lies in the first quadrant.
Therefore, $\tan 15{}^\circ $ is also positive.
$\therefore \tan 15{}^\circ =\dfrac{-2\sqrt{3}+4}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{\left( -\sqrt{3}+2 \right)}{{}}$
$\therefore \tan 15{}^\circ =2-\sqrt{3}$
Hence, the value of $\tan 15{}^\circ $ is $2-\sqrt{3}$ .
Note: Other useful formulas include:
$\tan (A+B)=\dfrac{\tan A+\tan B}{1-\tan A\tan B}$
$\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$
And you are free to use any formula, just substitute the angles according to the need to get the desired values.
We can also find the value of $\tan 15{}^\circ $ using formula: $\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$ .
On Substituting A and B in the above formula, we get;
$A=45{}^\circ $
$B=30{}^\circ $
The equation becomes:
$\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$
$\Rightarrow \tan (45{}^\circ -30{}^\circ )=\dfrac{\tan 45{}^\circ -\tan 30{}^\circ }{1+\tan 45{}^\circ \tan 30{}^\circ }$
\[\Rightarrow \tan 15{}^\circ =\dfrac{1-\left( \dfrac{1}{\sqrt{3}} \right)}{1+1\times \dfrac{1}{\sqrt{3}}}\]
Point to remember: whenever you try to find the value of $\sin 15{}^\circ $ , don’t use the formula of $\sin 2A$ , instead, go for the formula: $\cos 2A=1-2{{\sin }^{2}}A$ . The reason being, whenever you use the formula of $\sin 2A$ , you get both $\cos A$ and $\sin A$ to be unknown, making it difficult to solve.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Pomato is a Somatic hybrid b Allopolyploid c Natural class 12 biology CBSE




