If \[{\text{A}} = \{ 10,15,20,25,30,35,40,45,50\} \],
\[{\text{B}} = \{ 1,5,10,15,20,30\} \] and
\[{\text{C}} = \{ 7,8,15,20,35,45,48\} ,\] find \[{\text{A}} - ({\text{B}} \cap {\text{C}})\].

Hint:- Draw Venn’ diagram. First find \[{\text{B}} \cap {\text{C}}\].


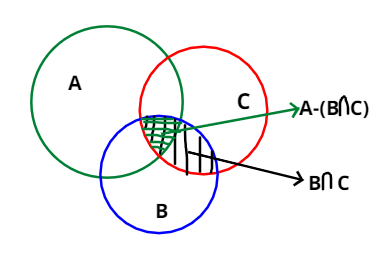
As, we are given with three sets and that were,
\[ \Rightarrow {\text{A}} = \{ 10,15,20,25,30,35,40,45,50\} ,\]
\[ \Rightarrow {\text{B}} = \{ 1,5,10,15,20,30\} \] and
\[ \Rightarrow {\text{C}} = \{ 7,8,15,20,35,45,48\} \]
And asked to find \[{\text{A}} - ({\text{B}} \cap {\text{C}})\].
And as we know that in set theory \[ \cap \] depicts intersection.
\[ \Rightarrow \]An intersection of two sets gives us the common elements of both sets.
So, \[{\text{B}} \cap {\text{C}}\] will give us common elements of sets B and C
\[ \Rightarrow \]So, \[{\text{(B}} \cap {\text{C) }} = {\text{ }}\{ 1,5,10,15,20,30\} \cap \{ 7,8,15,20,35,45,48\} = \{ 15,20\} \]
As we know that if X and Y are some sets then,
\[ \Rightarrow \]X-Y will give us a set having all elements of X excluding elements of Y.
So, \[{\text{A}} - ({\text{B}} \cap {\text{C}})\] will give us those elements of set A which are not in set \[{\text{(B}} \cap {\text{C)}}\]
\[ \Rightarrow \]\[{\text{A}} - ({\text{B}} \cap {\text{C}}) = \{ 10,15,20,25,30,35,40,45,50\} - \{ 15,20\} \]
\[ \Rightarrow \]Hence, \[{\text{A}} - ({\text{B}} \cap {\text{C}}) = \{ 10,25,30,35,40,45,50\} \]

Note:- Whenever we come up with this type of problem then first, we have to Draw Venn’s diagram because this will give proper clarity for the problem. Then remember that for any set X and Y, X-Y will give us a set having all elements of
X excluding elements of Y.