Name the angles in the given figure.

Hint: We will look at the basic definition of angles and then find the angles respectively. An angle is basically the space between two intersecting lines or surfaces close to the point where they meet.

Complete step-by-step solution -
In the above figure, we have two intersecting lines $AC$ and $BD$ that are intersecting at $O$ and four angles are formed by them, namely, $\angle AOB,\angle AOD,\angle DOC$ and $\angle COB$.

It is given in the question that we have to name the angles in the given figure.

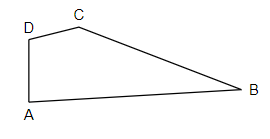
To name the angles, we have to recall the basic definition of angles and how those angles can be represented. So, angle is the space between two intersecting lines or surfaces close to the point where they meet.

Let us consider the triangle in the figure above. In the triangle $ABC$, we have three angles, namely, $\angle ABC,\angle BCA$ and $\angle CAB$. Now let us consider the figure given in our question. We will name the angles in the given diagram as follows,

So, looking at the figure, we can make out that it is a quadrilateral with four sides, $AB,BC,CD$ and $DA$ with angles, which we have to name. So, we can name the angles in the following manner. Angle 1 can be named as $\angle DAB$. It is an acute angle as it seems to be less than 90 degrees.
Angle 2 can be named as $\angle ABC$. It is an acute angle as it seems to be less than 90 degrees.
Angle 3 can be named as $\angle BCD$. It is an obtuse angle as it seems to be greater than 90 degrees.
Angle 4 can be named as $\angle CDA$. It is an obtuse angle as it seems to be greater than 90 degrees.
Hence, we have named the angles of the given figure.

Note: The students may get confused by thinking that $\angle DAB$ and $\angle BAD$ are different angles, but actually they are the same as they are representing the same $\angle A$. The concept is that while we are naming angles, we consider only the central alphabet that is on the vertex and the other two alphabets are the intersecting sides that can be interchanged. For example, in $\angle 2$, the vertex is at $B$, so it can be represented as either $\angle ABC$ or as $\angle CBA$. Both are the same.