What is the side of the square whose area is 36 sq cm?

Hint: Assume a variable (say x cm) for the length of the side of the square. Area of the square will be ${{x}^{2}}c{{m}^{2}}$ equate ${{x}^{2}}c{{m}^{2}}$ with the given area of the square and then solve for x.

Complete step-by-step answer:
According to the question, there is a square with area $36c{{m}^{2}}$ and we have to find the length of the side of this square.
Let us assume the length of the side of the square =x cm.

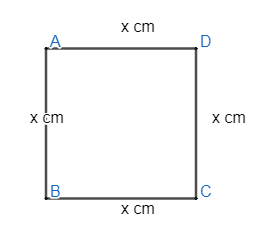
We know that area of square $={{\left( side \right)}^{2}}$ .
So, the area of the square length of whose sides are ‘x’ cm will be ${{x}^{2}}c{{m}^{2}}$ .
But according to the question, the area of the square =$36c{{m}^{2}}$.
So, ${{x}^{2}}=36c{{m}^{2}}$ .
Taking positive square root of both sides of the equation, we will get
$\Rightarrow x=6cm$ .
Hence the required side of the given square is 6cm.

Note: While solving the equation ${{x}^{2}}=36c{{m}^{2}}$ in the solution, we have taken only positive square root because ‘x’ is the length of a side and length of side of a square cannot be negative.