The minimum value of $\mu $ for which the system remains at rest once it has stopped for the first time is:

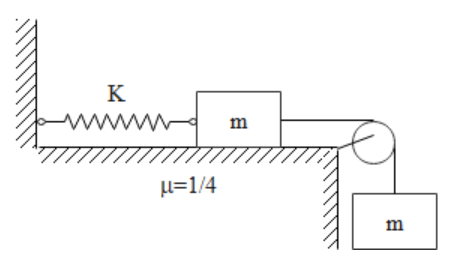
$\begin{array}{l}
{\rm{A}}{\rm{. }}\dfrac{1}{{\sqrt 3 }}\\
{\rm{B}}{\rm{. }}\dfrac{1}{3}\\
{\rm{C}}{\rm{. }}\dfrac{1}{2}\\
{\rm{D}}{\rm{. }}\dfrac{1}{{\sqrt 2 }}
\end{array}$

Hint: First we need to draw the free body diagram for the given system which will tell us about the various forces acting on this system. On the basis of the diagram, we need to write equations of motion for the system. Solving these equations, we may obtain the required answer.

Complete step-by-step answer:
Let us draw the free body diagram for the given system of masses and the spring.

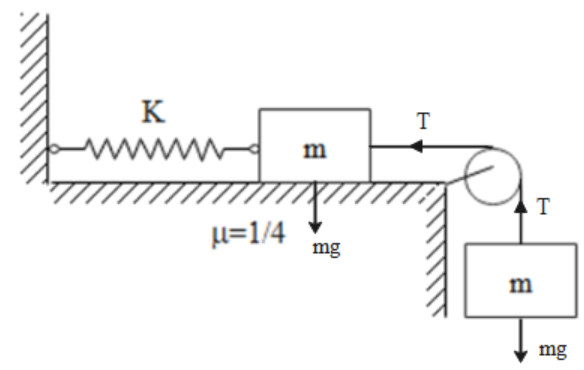
The various forces acting on the system involve the force due to weights of the masses and corresponding tension T in the string and a force due to stretching of the spring of force constant K.
There is motion in the system towards the right as the spring stretches.
For the first block ( one that is directly connected to the spring ), we can write the following equation:
\[T - \mu mg - kx = ma{\rm{ }}...\left( i \right)\]
Here T is the tension in the string, $\mu $ is the coefficient of friction between the block and the surface while a is the acceleration of the mass.
Similarly, we can write the following equation for the second mass:
$mg - T = ma{\rm{ }}...\left( {ii} \right)$
Now we want to see what happens when acceleration of the system becomes zero. Then a = 0, by using this in equations (i) and (ii), we get
\[\begin{array}{l}
T - \mu mg - kx = 0\\
 \Rightarrow T = \mu mg + kx\\
\& {\rm{ }}mg - T = 0\\
 \Rightarrow T = mg
\end{array}\]
Now we can write the two equations in the following way.
$mg = \mu mg + kx$
As the spring stretches towards the right direction, the system starts to decelerate and eventually the two masses will come to rest. We can find out the elongation in the spring as the masses come to rest. Using the work-energy theorem, we get
$\begin{array}{l}
{W_{gravity}} + {W_{friction}} + {W_{spring}} = \Delta K.E.\\
mg \times x - \mu mg \times x + \dfrac{1}{2}k{x^2} = 0\\
k{x^2} + 2x\left( {mg - \mu mg} \right) = 0\\
x = \dfrac{{2mg\left( {1 - \mu } \right)}}{k}
\end{array}$
Now when the spring reaches its maximum elongation, then the mass on the table will start moving towards the left. There is friction acting on the mass as it moves towards the left which will keep the mass stationary.
$kx = mg + \mu mg$
Using the value of elongation obtained earlier, the minimum value of coefficient of friction requires
$\begin{array}{l}
k\left( {\dfrac{{2mg\left( {1 - \mu } \right)}}{k}} \right) = mg + \mu mg\\
2\left( {1 - \mu } \right) = 1 + \mu \\
2 - 2\mu = 1 + \mu \\
3\mu = 1\\
\mu = \dfrac{1}{3}
\end{array}$
Hence, the minimum value of coefficient of friction required is $\dfrac{1}{3}$. Hence, the correct answer is option B.

Note: 1. The two masses undergo the same acceleration.
2. The tension in the string is equal to the mass of the block.
3. In work energy theorem expression, kinetic energy is zero as we consider the system to be at rest.