Gravitation Class 11 Notes CBSE Physics Chapter 7 (Free PDF Download)

Summary - Class 11 Physics Gravitation Notes (Chapter 7) 

1. Introduction

The constituents of the universe are galaxies, stars, planets, comets, asteroids, meteoroids. The force which keeps them bound together is called gravitational force. Gravitation is a natural phenomenon by which material objects attract one another.

In 1687 A.D. English Physicist Sir Isaac Newton published the book, Principia Mathematica, which explains the inverse-square law of gravitation.

2. Newtons Law of Gravitation

2.1. Definition

Every particle of matter attracts every other particle of matter with a force that is proportional to the product of their masses and inversely proportional to the square of their separation.

2.2. Mathematical Form

If ${m_1}$and ${m_2}$are the masses of the particles and r is the distance between them, the force of attraction $F$between the particles is given by: 

\[F \propto \dfrac{{{m_1}{m_2}}}{{{r^2}}}\]

\[\therefore\:F = G\dfrac{{{m_1}{m_2}}}{r}\].

(G is the universal constant of gravitation.)

2.3. Vector Form

In vector form, Newton’s law of gravitation is represented in the following manner. The force \[\left( \vec {F_{21}}\right)\] exerted on the particle ${m_2}$ by the particle ${m_1}$ is given by: 

\[\vec {F_{21}}=- G\:\dfrac{{m_1}{m_2}}{r^2}\:\hat{r_{12}}\]        …(1)

Where (\[\hat {r_{12}}\]) is a unit vector drawn from particle ${m_1}$ to particle ${m_2}$.

Similarly, the force \[\left( \vec {F_{12}} \right)\] exerted on particle ${m_1}$ by particle ${m_2}$ is given by:  

\[\vec {F_{12}}\:=\:+\;G\:\dfrac{{m_1}{m_2}}{r^2}\:\hat {r_{12}}\]      …(2)

Where (\[\hat {r_{12}}\]) is a unit vector drawn from particle ${m_1}$ to particle ${m_2}$.

From (1) and (2):

\[\vec {F_{12}}=  - \vec {F_{21}}\] 

3. Universal Constant for Gravitation

Universal gravitation constant is given as, \[{\text{G}} = \dfrac{{{\text{F}}{{\text{r}}^2}}}{{{{\text{m}}_1}{{\text{m}}_2}}}\]

Suppose that, 

\[{m_1}{\text{ }} = {\text{ }}{m_2}{\text{ }} = {\text{ }}1\], 

and 

\[r{\text{ }} = {\text{ }}1{\text{ }}then{\text{ }}G{\text{ }} = {\text{ }}F\].

The force of attraction between two unit masses put at a unit distance apart is numerically equal to the universal gravitation constant.

3.1. Unit

SI unit: \[\dfrac{{{\text{newton}}{{({\text{metre}})}^2}}}{{{{({\text{kilogram}})}^2}}} = \dfrac{{{\text{N}}{{\text{m}}^2}}}{{{\text{k}}{{\text{g}}^2}}}\]     

CGS Unit: 

\[{\text{dynec}}{{\text{m}}^2}/{\text{g}}{{\text{m}}^2}\].

3.2. Value of G

The value of G: 

\[{\text{G}} = 6.67 \times {10^{ - 11}}{\text{N}}{{\text{m}}^2}/{\text{k}}{{\text{g}}^2}\] 

Dimensions of G:

\[[{\text{G}}] = \dfrac{{[{\text{F}}]\left[ {{{\text{r}}^2}} \right]}}{{\left[ {{{\text{m}}_1}{{\text{m}}_2}} \right]}}\]= \[\dfrac{{\left[ {{{\text{M}}^1}{{\text{L}}^1}{{\text{T}}^2}} \right]\left[ {{{\text{M}}^0}{{\text{L}}^2}{{\text{T}}^0}} \right]}}{{\left[ {{{\text{M}}^2}{{\text{L}}^0}{{\text{T}}^0}} \right]}}\] \[ = \left[ {{{\text{M}}^{ - 1}}{{\text{L}}^3}{{\text{T}}^{ - 2}}} \right]\]

Notes:

1. The gravitational force is independent of the intervening medium.

2. The gravitational force is a conservative force. 

3. The first particle exerts a force on the second that is exactly equal to and opposite to the second particle's force on the first.

4. The gravitational force between two particles acts along the line that connects them, and they are part of an action-reaction pair.

4. Variation in ‘g’

4.1. The Acceleration Due to Gravity at a Height h above the Earth’s Surface

Let M and R be the earth's mass and radius, respectively, and g denote the acceleration due to gravity at the surface. Assume that a mass of m is placed on the earth's surface.

The weight ‘mg’ of the body is equal to the gravitational force acting on it.

\[mg = \dfrac{{GMm}}{{{R^2}}}\]  

\[\Rightarrow g = \dfrac{{GM}}{{{R^2}}}\]         …(1)

Now suppose that the body is raised to a height \[h\], above the earth’s surface, the weight of the body is now \[mg\] and the gravitational force acting on it is: 

\[\dfrac{{{\text{GMm}}}}{{{{({\text{R}} + {\text{h}})}^2}}}\]

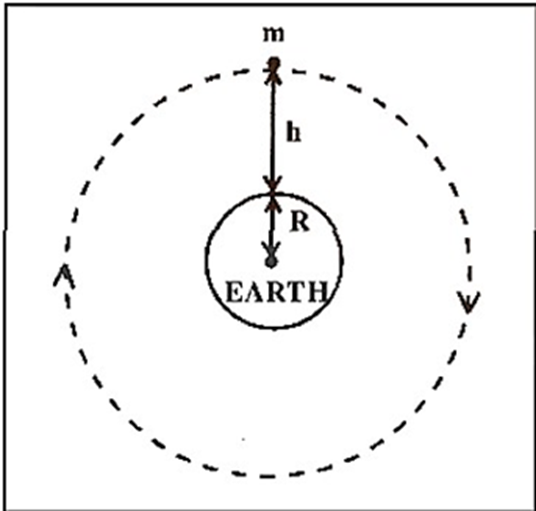
\[\therefore\:{\text{m}}{{\text{g}}_{\text{h}}} = \dfrac{{{\text{GMm}}}}{{{{({\text{R}} + {\text{h}})}^2}}}\] 

\[{g_h} = \dfrac{{GM}}{{{{(R + h)}^2}}}\]       …(2)

Dividing eq (2) by eq (1), we get,  

\[\dfrac{{{{\text{g}}_{\text{h}}}}}{{\text{g}}} = \dfrac{{{{\text{R}}^2}}}{{{{({\text{R}} + {\text{h}})}^2}}}\]

\[\Rightarrow\:{{\text{g}}_{\text{h}}} = \left[ {\dfrac{{{{\text{R}}^2}}}{{{{({\text{R}} + {\text{h}})}^2}}}} \right]{\text{g}}\] .

4.2.  Acceleration due to Gravity at a Very Small Height

\[{g_h} = g{\left( {\dfrac{{R + h}}{R}} \right)^2}\] 

\[\Rightarrow {g_h} = g{\left( {1 - \dfrac{{\text{h}}}{{\text{R}}}} \right)^{ - 2}}\] 

\[\Rightarrow {g_h} = {\text{g}}\left( {1 - \dfrac{{2{\text{h}}}}{{\text{R}}} + \dfrac{{{{\text{h}}^2}}}{{{{\text{R}}^2}}} \ldots  \ldots .} \right)\] 

If h << R, then neglecting high power’s of ‘h’ we get:  

 \[{g_h} = g\left( {1 - \dfrac{{2h}}{R}} \right)\] .

4.3. Effect of Depth on a Acceleration due to Gravity

Also g in terms of ρ:  

\[{\text{g}} = \dfrac{{GM}}{{{{\text{R}}^2}}}\]

If ρ is density of the material of earth, then:  

\[{\text{M}} = \dfrac{4}{3}\pi {{\text{R}}^3}\rho \]                                                                              

\[{\text{g}} = \dfrac{{{\text{G}} \times \dfrac{4}{3}\pi {{\text{R}}^3}\rho }}{{{{\text{R}}^2}}}\]                                                               

\[g = \dfrac{4}{3}\pi {\text{GR}}\rho \]                 …(1)

Let \[{g_d}\] be the gravitational acceleration at point \[B\] at a depth \[x\] below the earth's surface. At point B, there is a body that will only be subjected to force as a result of the earth's part OB (\[R – d\]) radius. The outer spherical shell, whose thickness is d, will not exert any force on the body at point B. Because it will act as a shell and point is inside.

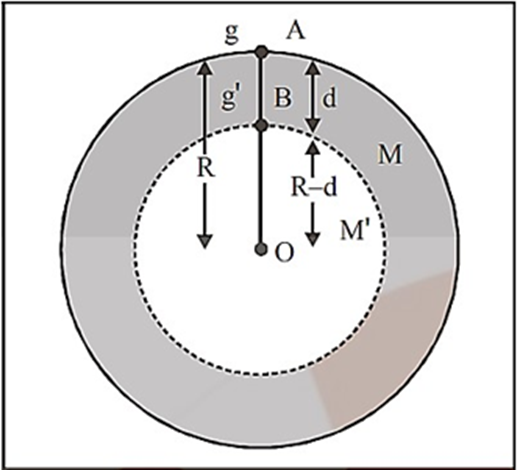
\[{\text{Now,}}M' = \dfrac{4}{3}\pi {(R - x)^3}\rho \]

Or       

\[{{\text{g}}_{\text{d}}} = _3^4\pi {\text{G}}({\text{R}} - {\text{d}})\rho \]               …(2)

Dividing the equation (2) by (1), we have:

\[\dfrac{{{{\text{g}}_d}}}{{\text{g}}} = \dfrac{{\dfrac{4}{3}\pi {\text{G}}({\text{R}} - {\text{d}})\rho }}{{\dfrac{4}{3}\pi {\text{GR}}\rho }}\]

\[ = \dfrac{{{\text{R}} - {\text{d}}}}{{\text{R}}}{\text{or}}{{\text{g}}_{\text{d}}} = {\text{g}}\left( {1 - \dfrac{{\text{d}}}{{\text{R}}}} \right)\]         …(3)

Therefore, the value of acceleration due to gravity decreases with depth.

4.4. Variation of ‘g’ with Latitude due to Rotational Motion of Earth

The force \[mr{\omega ^2}\cos \lambda \]acts radially outwards due to the earth's rotation. As a result, the net force of attraction exerted by the particle's earth and directed towards the earth's centre is provided by:

\[{\text{m}}{{\text{g}}^\prime } = {\text{mg}} - {\text{mr}}{\omega ^2}\cos \lambda \] .

where g’ is the value of the acceleration due to gravity at the point P.

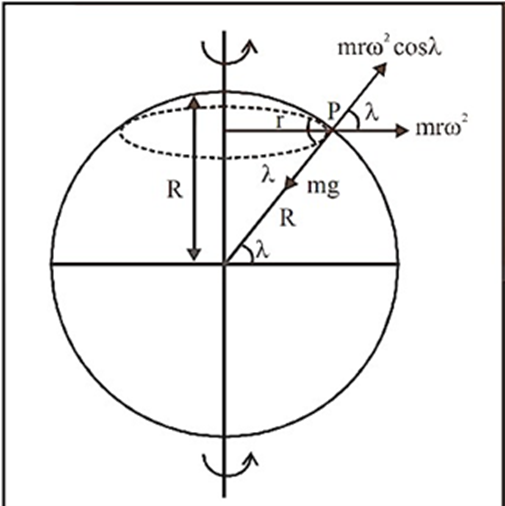
${g^\prime } = g - r{\omega ^2}\cos \lambda $

Now, ${\text{r}} = {\text{R}}\cos \lambda $ (where ${\text{R}}$ is the radius of the earth)

Then, 

\[{{\text{g}}^\prime } = {\text{g}} - ({\text{R}}\cos \lambda ){\omega ^2}\cos \lambda \] 

\[\therefore \quad {{\text{g}}^\prime } = {\text{g}} - {\text{R}}{\omega ^2}{\cos ^2}\lambda\]

The effective acceleration due to gravity at a point ‘P’ is given by: 

\[g' = g - R{\omega ^2}{\cos ^2}\lambda \]

Thus value of ‘g’ changes with ‘λ’ and ‘ω’. 

1. At Poles:

\[\lambda  = 90\]

\[{g^\prime } = g - R{\omega ^2}{\cos ^2}90\]

\[{g^\prime } = g \]

2. At Equator:

\[{\lambda  = 0} \]

\[{g' = g - R{\omega ^2}{{\cos }^2}0}\] 

\[{g' = g - R{\omega ^2}}\] 

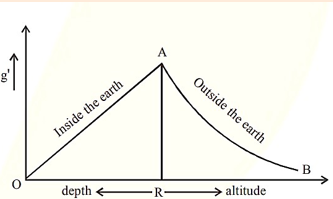
Note:

The variation of acceleration due to gravity according to the depth and the height from the earth’s surface can be expressed with the help of the following graph.

5. Satellite

5.1. Any Smaller Body which revolves around another larger body under the influence of its gravitation is called a satellite. It may be natural or artificial.

1. The moon is a satellite of the earth since it rotates around it. Jupiter has sixteen satellites that circling around it. Natural satellites are the name given to these satellites.

2. An artificial satellite is one that has been built and launched into circular orbit by humans. The USSR launched the first satellite, SPUTNIK–I, while India launched the first satellite, ARYABHATTA.

5.2. Minimum Two-Stage Rocket is Used to Project a Satellite in a Circular Orbit Around a Planet

Assume that a single-stage launching system (i.e., a rocket) is utilised to launch a satellite from the earth's surface. The rocket begins to go upwards once the fuel in the rocket is ignited. When all of the fules has been used up, the rocket reaches its maximum velocity.

1. If the rocket's maximum velocity is equal to or greater than the escape velocity, the rocket escapes into space with the satellite, overcoming the earth's gravitational effect.

2. If the rocket's maximum velocity is less than escape velocity, it will be unable to resist the earth's gravitational pull, and both the rocket and the satellite will eventually descend to the earth's surface owing to gravity.

As a result, a single-stage rocket cannot put a satellite into a circular orbit around the globe. As a result, to launch a satellite into a circular orbit around the earth, a launching device (i.e., a rocket) with two or more stages must be used.

5.3. Different Cases of Projection:

Depending on the amount of the horizontal velocity, the following four instances may occur when a satellite is lifted to a certain height above the earth and then projected horizontally.

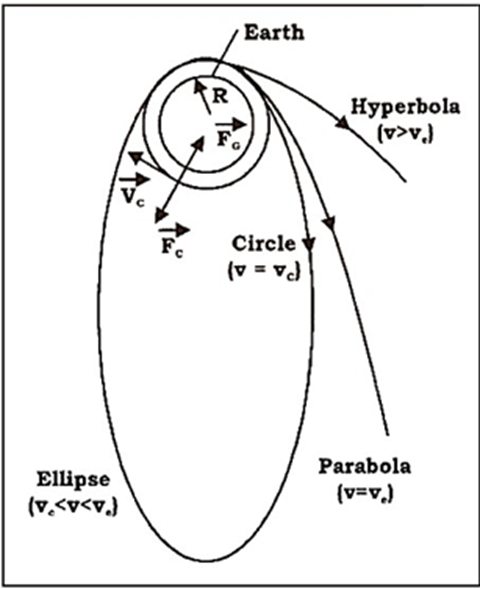
1. If the velocity of the projection is less than the critical velocity then the satellite moves in an elliptical orbit, but the point of projection is apogee and in the orbit, the satellite comes closer to the earth with its perigee point lying at \[180^o\]. If it enters the atmosphere while coming towards perigee it will lose energy and spirally comes down. If it does not enter the atmosphere it will continue to move in an elliptical orbit.

2. If the projection velocity equals the critical velocity, the satellite will move in a circular orbit around the planet.

3. If the projection velocity is more than the critical velocity but less than the escape velocity, the satellite will be in an elliptical orbit with an apogee, or farthest distance from the earth, larger than the projection height.

4. If the velocity of the projection is equal to the escape velocity, then the satellite moves in a parabolic path.

5. If the velocity of the projection is greater than the escape velocity, then the orbit will hyperbolic and will escape the gravitational pull of the earth and continue to travel infinitely.

6. Orbital Velocity

6.1. Definition 

The horizontal velocity with which a satellite must be projected from a point above the earth’s surface so that it revolves in a circular orbit around the earth is called the orbital velocity of the satellite.

6.2. An Expression for the Critical Velocity of a Satellite Revolving Around the Earth

Suppose that a satellite of mass m is raised to a height h above the earth’s surface and then projected in a horizontal direction with the orbital velocity ${v_c}$. The satellite begins to move around the earth in a circular orbit of radius, \[R{\text{ }} + {\text{ }}h\], where \[R\] is the radius of the earth.\[\]

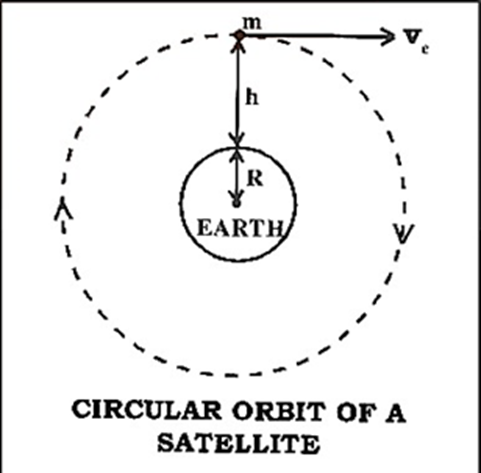
The gravitational force acting on the satellite is \[\dfrac{{{\text{GMm}}}}{{{{({\text{R}} + {\text{h}})}^2}}}\], where $M$ is the mass of the earth and $G$ is the constant of gravitation.

For circular motion,

Centrifugal force = Centripetal force

\[\dfrac{{{\text{mv}}_{\text{c}}^2}}{{({\text{R}} + {\text{h}})}} = \dfrac{{{\text{GMm}}}}{{{{({\text{R}} + {\text{h}})}^2}}}\]

\[\therefore \:{{\text{v}}_{\text{c}}} = \sqrt {\dfrac{{{\text{GM}}}}{{({\text{R}} + {\text{h}})}}} \] 

This expression gives the critical velocity of the satellite. From the expression, it is clear that the critical velocity depends upon.

1. Mass of the earth

2. The radius of the earth

3. Height of the satellite above the surface of the earth.

7. Height of the Satellite Above the Surface of the Earth

The time taken by a satellite to complete one revolution around the earth is called it’s period or periodic time (T).  Consider a satellite of mass m revolving in a circular orbit with a orbital velocity  \[{v_c}\] at a height h above the surface of the earth. Let \[M\] and \[R\] be the mass and the radius of the earth respectively.

The radius (r) of the circular orbit of the satellite is \[r = R + h\].

For the circular motion,

\[{v_c} = \sqrt {\dfrac{{{\text{GM}}}}{r}} \]      …(1)

If T is the period of revolution of the satellite,  

\[Period{\text{ }}\left( T \right)\, = \,\dfrac{{circumference\,of\,orbit}}{{critical\,velocity}} = \dfrac{{2\pi r}}{{{v_c}}}\]

\[\Rightarrow T\:=\:\dfrac {2\pi r}{\sqrt{\dfrac {GM}{r}}}\]

\[\Rightarrow {\text{T}} = 2\pi \sqrt {\dfrac{{{{\text{r}}^3}}}{{{\text{GM}}}}} \]

This expression gives the periodic time of the satellite. Squaring the expression, we get, 

\[{{\text{T}}^2} = {\dfrac{{4{\pi ^2}{{\text{r}}^3}}}{{GM}}}\]

\[{{\text{T}}^2}\alpha {{\text{r}}^3}\] ...(since G and M are constants)

Thus, the square of the period of revolution of a satellite is directly proportional to the cube of the radius of its orbit. 

Object	Potential$(V)$	Electric Field $(E)$	Figure
Ring	\[{\text{V}} = \dfrac{{ - {\text{GM}}}}{{{{\left( {{{\text{a}}^2} + {{\text{r}}^2}} \right)}^{1/2}}}}\]	\[\vec E = \dfrac{{ - {\text{GMr}}}}{{{{\left( {{{\text{a}}^2} + {{\text{r}}^2}} \right)}^{3/2}}}}{\mathbf{\hat r}}\]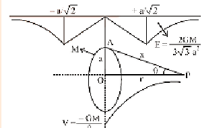
Thin Circular Ring	\[V = \dfrac{{ - 2GM}}{{{a^2}}}\left[ {\sqrt {{a^2} + {r^2}}  - r} \right]\]	\[\vec E =  - \dfrac{{2{\text{GM}}}}{{{{\text{a}}^2}}}\left[ {1 - \dfrac{{\text{r}}}{{\sqrt {{{\text{r}}^2} + {{\text{a}}^2}} }}} \right]{\mathbf{\hat r}}\]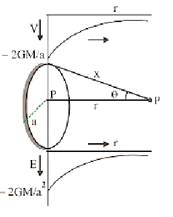
Uniform thin spherical shell a) Point P inside the shell ($r \leqslant a$)	\[{\text{V}} = \dfrac{{ - {\text{GM}}}}{{\text{a}}}\]	\[{\text{E}} = 0\]
b) Point P outside the shell ($r \geqslant a$)	\[{\text{V}} = \dfrac{{ - {\text{GM}}}}{{\text{r}}}\]	\[\vec E\:=\:-\;\dfrac {GM}{r^2}\;\hat {r}\]
Uniform solid sphere (a). Point P inside the sphere ($r \leqslant a$)	\[{\text{V}} =  - \dfrac{{{\text{Gm}}}}{{2{{\text{a}}^3}}}\left( {3{{\text{a}}^2} - {{\text{r}}^2}} \right)\]	\[{\vec E} = \dfrac{{ - {\text{GM}}}}{{{{\text{a}}^3}}}{\hat r}\]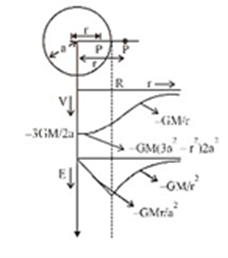
(b) Point P outside the shell ($r \geqslant a$)	\[{\text{V}} =  - \dfrac{{{\text{GM}}}}{{\text{r}}}\]	\[\vec E\:=\:-\;\dfrac {GM}{r^2}\;\hat {r}\]

Uniform Thick Sphere a) Point outside the shell	\[{\text{V}} =  - {\text{G}}\dfrac{{\text{M}}}{{\text{r}}}\]	\[{\vec E} =  - {\text{G}}\dfrac{{\text{M}}}{{{{\text{r}}^2}}}{\hat r}\]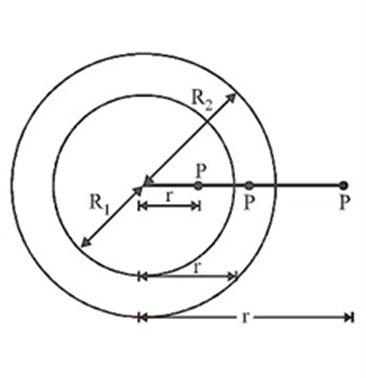
b) Point Inside the Shell	\[{\text{V}} = \dfrac{{ - 3}}{2}{\text{GM}}\left( {\dfrac{{{{\text{R}}_2} + {{\text{R}}_1}}}{{{\text{R}}_2^2 + {{\text{R}}_1}{{\text{R}}_2} + {\text{R}}_1^2}}} \right)\]	\[{\vec E} = 0\]
c) Point between the two surfaces	\[{\text{V}} = \dfrac{{ - {\text{GM}}}}{{2{\text{r}}}}\left( {\dfrac{{3{\text{rR}}_2^2 - {{\text{r}}^3} - 2{\text{R}}_1^3}}{{{\text{R}}_2^3 - {\text{R}}_1^3}}} \right)\]	\[{\vec E} = \dfrac{{ - {\text{GM}}}}{{{{\text{r}}^2}}}\left( {\dfrac{{{{\text{r}}^3} - {\text{R}}_1^3}}{{{\text{R}}_2^3 - {\text{R}}_1^3}}} \right){\hat r}\]

8. Gravitational Field

A gravitational field is the space that surrounds any mass. A gravitational pull acts on any additional mass introduced into this space. In a nutshell, the area in which a gravitational pull is experienced by any mass field of gravity. 

9. Gravitational Intensity

The gravitational intensity at any point in a gravitational field is defined as the force acting on a unit mass placed at that point.

1. The gravitational intensity ($E$) at a point at distance $r$from a point mass $M$is given by: \[E = \dfrac{{GM}}{{{r^2}}}\] (where $G$ is the constant of gravitation)

2. If a point mass $m$is placed in a gravitational field of intensity $E$, the force ($F$) acting on the mass $m$is given by: \[{\text{F}} = {\text{mE}}\].

10. Gravitational Potential 

The work required to transport a unit mass from infinity to any location in a gravitational field is defined as the gravitational potential at that point.

1. The gravitational potential ($V$) at a point at distance $r$ from a point mass $M$ is given by: 

\[\Rightarrow V=\dfrac {-GM}{r}\] 

(Where G is the constant of gravitation)

2. The work done on a unit mass is converted into its potential energy. Thus, the gravitational potential at any point is equal to the potential energy of a unit mass placed at that point. 

3. If a small point mass m is placed in a gravitational field at a point where the gravitational potential is V, the gravitational potential energy (P.E.) of the mass m is given by: 

\[{\text{P}}{\text{.E}}{\text{.}} = {\text{mass}} \times {\text{gravitational potential}}\]\[ = {\text{mV}}\]

\[{\text{P}}{\text{.E}}{\text{.}} =  - \dfrac{{GMm}}{r}\]

10.1. Gravitational Potential Energy

The work done in taking a body from infinity to a specific point is defined as gravitational potential energy.

Let a body of mass $m$is displaced through a distance ‘$dr$’ towards the mass $M$, then work done given by: 

\[{\text{dW}} = {\text{Fdr}} = \dfrac{{{\text{GM}}{{\text{m}}_{}}}}{{{{\text{r}}^2}}}{\text{dr}}\]

Gravitational potential energy, 

\[{\text{U}} =  - \dfrac{{{\text{GMm}}}}{{\text{r}}}\] .

1. From above equation, it is clear that gravitational potential energy increases with increase in distance (\[r\]) (i.e. it becomes less negative).

2. Gravitational P.E. becomes maximum (or zero) at \[r = \infty \].

10.2. Expressions for Different Energies of Satellite

1. Potential Energy

2. Kinetic Energy

3. Total Energy

4. Binding energy

Let 

\[M\]= mass of the earth 

\[R\]= radius of the earth 

\[m\]= mass of the satellite 

\[G\]= constant of gravitation

\[h\]= height of satellite

1. Potential Energy (P.E.): 

The satellite is at a distance (R + h) from the centre of the earth.

\[{\text{U}} =  - \dfrac{{{\text{G}}{{\text{m}}_1}{{\text{m}}_2}}}{{\text{r}}}\] 

\[\Rightarrow - \dfrac{{{\text{GMm}}}}{{{\text{R}} + {\text{h}}}} = {\text{U}}\]

2. Kinetic Energy (K.E.) : 

The satellite is revolving in a circular orbit with the critical velocity (vc). Hence its kinetic energy is given by: 

\[{\text{K}}.{\text{E}}. = \dfrac{1}{2}{\text{mv}}_{\text{c}}^2\]

\[{v_c}\:=\:\sqrt{\dfrac {GM}{R+h}}\]

\[\Rightarrow K.E. = \dfrac{1}{2}m\left( {\dfrac{{GM}}{{{\text{R}} + {\text{h}}}}} \right) = \dfrac{{{\text{GMm}}}}{{2({\text{R}} + {\text{h}})}}\] 

3. Total Energy (T.E.):   

T.E = P.E. + K.E

\[T.E =  - \dfrac{{{\text{GMm}}}}{{{\text{R}} + {\text{h}}}} + \dfrac{{{\text{GMm}}}}{{2({\text{R}} + {\text{h}})}} =  - \dfrac{{{\text{GMm}}}}{{2({\text{R}} + {\text{h}})}}\] 

The \[-ve\] sign indicates that the satellite is bound to the earth.

4. Binding Energy (B.E.): 

From the expression for the total energy, it is clear that if the satellite is given energy equal to \[ + \dfrac{{{\text{GMm}}}}{{2({\text{R}} + {\text{h}})}}\] the satellite will escape to infinity where its total energy is zero.          

\[{\text{B}}{\text{.E}}{\text{.}} =  - ({\text{T}}{\text{.E}}{\text{.}}) =  - \left[ { - \dfrac{{{\text{GMm}}}}{{2({\text{R}} + {\text{h}})}}} \right] =  + \dfrac{{{\text{GMm}}}}{{2({\text{R}} + {\text{h}})}}\]

5. Binding Energy of a Satellite: 

The minimum energy which must be supplied to a satellite, so that it can escape from the earth’s gravitation field, is called the binding energy of a satellite. When the body of mass m is at rest on the earth’s surface, its gravitational potential energy is given by:

\[{\text{U}} =  - \dfrac{{GMm}}{{\text{R}}}\]  

If the body is give an energy equal to: \[ + \dfrac{{{\text{GMm}}}}{{\text{R}}}\] it will escape to infinity.

Binding energy of the body\[ + \dfrac{{{\text{GMm}}}}{{\text{R}}}\]

11. Escape Velocity of a Body

11.1. Expression for the Escape Velocity of a Body at Rest on the Earth’s Surface

The escape velocity is the lowest velocity at which a body should be ejected from the earth's surface in order to escape the gravitational field of the planet velocity.

Thus, if a body or a satellite is given the escape velocity, its kinetic energy of projection will be equal to its binding energy.

Kinetic Energy of projection = Binding Energy

\[\dfrac{1}{2}{\text{mv}}_{\text{e}}^2 = \dfrac{{{\text{GMm}}}}{r}\]

\[\Rightarrow {{\text{v}}_{\text{e}}} = \sqrt {\dfrac{{2{\text{GM}}}}{{\text{R}}}} \]

11.2. Expression for ‘\[{V_e}\]’ in term’s of ‘\[g\]’

The escape velocity for any object on the earth’s surface is given by:\[{{\text{v}}_{\text{e}}} = \sqrt {\dfrac{{2{\text{GM}}}}{{\text{R}}}} \]

If m is the mass of the object, its weight mg is equal to the gravitational force acting on it.

\[{\text{mg}} = \dfrac{{{\text{GMm}}}}{{{R^2}}}\]  

\[{\text{G}}{\text{.M}} = {\text{g}}{{\text{R}}^2}\] 

Substituting this value in the expression for \[{V_e}\]we get, \[{{\text{v}}_{\text{e}}} = \sqrt {2{\text{gR}}} \]

11.3. Expression for the Escape Velocity of a Body from Earth in Terms of Mean Density of the Planet

1. Derive expression for  \[{v_e} = \sqrt {\dfrac{{2GM}}{R}} \]

2. Let ρ be the mean density of the planet. Then, \[{\text{M}} = \dfrac{4}{3}\pi {{\text{R}}^3}\rho \] 

\[{{\text{v}}_{\text{e}}} = \sqrt {\dfrac{{2{\text{G}}}}{{\text{R}}} \times \dfrac{4}{3}\pi {{\text{R}}^3}\rho } \]  

\[\Rightarrow {{\text{v}}_{\text{e}}} = 2{\text{R}}\sqrt {\dfrac{{2\pi {\text{G}}\rho }}{3}} \]

11.4. The Escape Velocity of a Body from the Surface of the Earth is 2 Times its Critical Velocity When it Revolves Close to the Earth’s Surface 

Let M and R be the earth's mass and radius, respectively, and m be the body's mass. The radius of the orbit is nearly equal to R while orbiting close to the earth's surface. If ${v_c}$ is the body's critical velocity, then the orbit is circular.

Centripetal force = Gravitational force

\[{\text{mv}}_{\text{c}}^2 = \dfrac{{{\text{GMm}}}}{{{R^2}}}\]

\[\Rightarrow {{\text{v}}_{\text{c}}} = \sqrt {\dfrac{{{\text{GM}}}}{{\text{R}}}} \]         …(1)

If \[{v_e}\]is the escape velocity from the earth’s surface, 

K.E. of projection = Binding energy \[{m_G}\]

\[\dfrac{1}{2}{\text{mv}}_{\text{e}}^2 = \mathop {\dfrac{{{\text{GMm}}}}{{{R^2}}}}\limits_{} \] 

\[\therefore {{\text{v}}_{\text{e}}} = \sqrt {\dfrac{{2{\text{GM}}}}{{\text{R}}}} \]              …(2)

From Eq (1) and Eq. (2), we get,       

\[{{\text{v}}_{\text{e}}} = \sqrt 2 {{\text{v}}_{\text{c}}}\]

12. Communication Satellite

An artificial satellite that revolves in a circular orbit around the earth in the same sense as the earth's rotation and has the same period of revolution as the earth's rotation(\[{\text{i}}{\text{.e}}{\text{.}}1{\text{day}} = 24{\text{hours}} = 86400{\text{seconds}}\]) is called as geo-stationary or communication satellite.

As the relative velocity of the satellite with respect to the earth is zero it appears stationary from the earth’s surface. Therefore it is known as a geostationary satellite or geosynchronous satellite.

1. The height of the communication satellite above the earth’s surface is about \[36000{\text{ }}km\] and its period of revolution is \[24{\text{ }}hours{\text{ }}or{\text{ }}24{\text{ }} \times {\text{ }}60{\text{ }} \times {\text{ }}60{\text{ }}seconds\].

2. The satellite appears to be at rest, because its speed relative to the earth is zero, hence it is called as geostationary or geosynchronous satellite.

12.1. Uses of the Communication Satellite

1. For sending TV signals over large distances on the earth’s surface

2. Telecommunication.

3. Weather forecasting.

4. For taking photographs of astronomical objects.

5. For studying of solar and cosmic radiations.

13. Weightlessness

1. The weight of a body refers to the gravitational force that pulls it towards the earth's centre a feeling of weightlessness is like a moving satellite. It isn't because the weight is zero.

2. When an astronaut is on the surface of the earth, a gravitational force acts on him. This gravitational force is the weight of an astronaut and an astronaut exerts this force on the surface of the earth. The surface of the earth exerts an equal and opposite reaction and due to this reaction, he feels his weight on the earth.

3. for an astronaut in an orbiting satellite, the satellite and astronaut both have the same acceleration towards the centre of the earth and this acceleration is equal to the acceleration due to the gravity of the earth.

4. As a result, astronaut does not have any effect on the satellite's floor. Naturally, the astronaut is unaffected by the floor's reaction force. The astronaut experiences a sense of weightlessness since there is no reaction. (i.e. he has no idea how heavy he is).

Note: 

1. The sensation of weightlessness experienced by an astronaut is not the result of there being zero gravitational acceleration, but of there being zero difference between the acceleration of the spacecraft and the acceleration of the astronaut.

2. The most common problem experienced by astronauts in the initial hours of weightlessness is known as space adaptation syndrome (space sickness).

14. Kepler’s Laws

14.1. Law of Orbit

Each Planet move surrounds the sun in an elliptical orbit with the sun at one of the foci as shown in the figure. The eccentricity of an ellipse is defined as the ratio of the distance SO and AO i.e. 

\[e = \dfrac{{SO}}{{AO}}\]

\[e = \dfrac{{SO}}{a}\]  

\[\Rightarrow SO = ea\]

The distance of the closest approach with the sun at F1 is AS. This distance is called perigee. The greatest distance (BS) of the planet from the sun is called apogee. 

Perigee (AS) = AO – OS = \[a{\text{ }}--{\text{ }}ea{\text{ }} = {\text{ }}a{\text{ }}\left( {1{\text{ }}--{\text{ }}e} \right)\]

apogee (BS) = OB + OS = \[a{\text{ }} + {\text{ }}ea{\text{ }} = {\text{ }}a{\text{ }}\left( {1{\text{ }} + {\text{ }}e} \right)\]

14.2 Law of Area

The line joining the sun and a planet sweeps out equal areas in equal intervals of time. A planet takes the same time to travel from A to B as from C to D as shown in figure. (The shaded areas are equal). Naturally, the planet has to move faster from C to D.

\[Area\,velocity = \,\dfrac{{Area\,swept}}{{time}}\]\[ = \dfrac{{\dfrac{1}{2}{\text{r}}({\text{rd}}\theta )}}{{{\text{dt}}}} = \dfrac{1}{2}{{\text{r}}^2}\dfrac{{{\text{d}}\theta }}{{{\text{dt}}}} = {\text{constant}}\] 

Hence, \[\dfrac{1}{2}{r^2}\omega  = {\text{constant}}\] 

14.3. Law of Periods

The square of the time for the planet to complete a revolution about the sun is proportional to the cube of the semimajor axis of the elliptical orbit.

i.e. Centripetal force = Gravitational force

\[\dfrac{{{\text{m}}{{\text{v}}^2}}}{{\text{R}}} = \dfrac{{{\text{GMm}}}}{{{{\text{R}}^2}}} \Rightarrow \dfrac{{{\text{GM}}}}{{\text{R}}} = {{\text{v}}^2}\]

Now, velocity of the planet is, 

\[v = \dfrac{{circumference\,of\,the\,circular\,orbit}}{{Time\,Period}} = \dfrac{{2\pi R}}{T}\]

Substituting Value in above equation 

\[\dfrac{{{\text{GM}}}}{R} = \dfrac{{4{\pi ^2}{{\text{R}}^2}}}{{{{\text{T}}^2}}}\]  

or  

\[{{\text{T}}^2} = \dfrac{{4{\pi ^2}{{\text{R}}^3}}}{{{\text{GM}}}}\]

Since, \[\left( {\dfrac{{4{\pi ^2}}}{{GM}}} \right)\] is constant.

\[\therefore {{\text{T}}^2} \propto {{\text{R}}^3}\] or  \[\dfrac{{{{\text{T}}^2}}}{{{{\text{R}}^3}}} = {\text{constant}}\]

14.4.  Gravity 

The force of attraction exerted by the earth towards its centre on a body lying on or near the surface of the earth is known as gravity. Gravity is a type of gravity that is also known as the earth's gravitational pull.

Weight of a body is defined as the force of attraction exerted by the earth on the body towards its centre. The units and dimensions of gravity pull or weight are the same as those of force.

Launching of An Artificial Satellite Around the Earth:

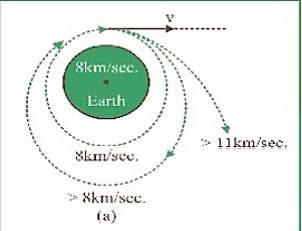
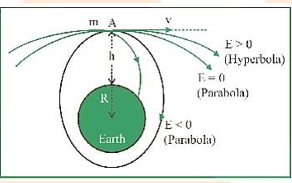
The satellite is placed upon the rocket which is launched from the earth. After the rocket reaches its maximum vertical height h, a spherical mechanism gives a thrust to the satellite at point A (figure) producing a horizontal velocity \[v\]. The total energy of the satellite at A is thus,

\[E = \dfrac{1}{2}m{v^2} - \dfrac{{GMm}}{{{\text{R}} + h}}\] 

The orbit will be an ellipse (closed path), a parabola, or a hyperbola depending on whether E is negative, zero, or positive. In all cases, the centre of the earth is at one focus of the path. If the energy is too low, the elliptical orbit will intersect the earth and the satellite will fall back. Otherwise it will keep moving in a closed orbit, or will escape from the earth, depending on the values of v and R. Hence a satellite carried to a height \[h{\text{ }}\left( { <  < {\text{ }}R} \right)\] and given a horizontal velocity of \[8{\text{ }}km/sec\] will be placed almost in a circular orbit around the earth (figure). If launched at less than \[8{\text{ }}km/sec\], it would get closer and closer to earth until it hits the ground. Thus \[8{\text{ }}km/sec\] is the critical (minimum) velocity.

14.5. Inertial Mass

Newton's second law of motion defines a body's inertial mass, which is related to its inertia in linear motion.

Let a body of mass mi move with acceleration a under the action of an external force F. According to Newton’s second law of motion, \[{\text{F}} = {{\text{m}}_{\text{i}}}{\text{a or}}{{\text{m}}_{\text{i}}} = {\text{F}}/{\text{a}}\] 

As a result, a body's inertial mass is equal to the magnitude of external force necessary to produce unit acceleration.

14.6. Gravitational Mass

The gravitational mass of a body is related to the gravitational pull on the body and is defined by Newton’s law of gravitational. 

\[{\text{F}} = \dfrac{{{\text{GM}}{{\text{m}}_{\text{G}}}}}{{{{\text{R}}^2}}}\]  or  

\[{{\text{m}}_{\text{G}}} = \dfrac{{\text{F}}}{{\left( {{\text{GM}}/{{\text{R}}^2}} \right)}} = \dfrac{{\text{F}}}{{\text{I}}}\]. 

The mass \[{m_G}\] of the body in this sence is the gravitational mass of the body. The intertia of the body has no effect on the gravitational mass of the body. \[{{\text{m}}_{\text{G}}} = {\text{F}}\]

Thus, the Gravitational mass of a body is defined as the magnitude of gravitational pull experienced by the body in a gravitational field of unit intensity.

14.7. Centre of Gravity

The Centre of gravity of a body placed in the gravitational field is the point where the net gravitational force of the field acts.

Gravitation Class 11 Notes Physics - Basic Subjective Questions

Section-A (1 Mark Questions)

1. Why is gravitational potential energy always negative?

Ans. Gravitational potential energy is always negative because gravitational force is always attractive.

2. At what height above the surface of the earth the value of acceleration due to gravity is reduced to one-fourth of its value on the surface of the earth?

Ans. $g_{h}=\dfrac{g}{4}=g\left ( \dfrac{R}{R+h} \right )^{2}$

$\dfrac{R}{R+h}=\dfrac{1}{\sqrt{4}}=\dfrac{1}{2}$

2R – R = h

h = R

3. Name two factors that determine whether a planet has an atmosphere or not. 

Ans.

(1) Acceleration due to gravity at the surface of the planet

(2) Surface temperature of the planet.

4. The gravitational force between two blocks is F. What would happen if the mass of both the blocks as well as the distance between them is doubled?

Ans. We know $F=\dfrac{Gm_{1}m_{2}}{r^{2}}$

When the mass of both the blocks and the distance between them are doubled

$\Rightarrow F=\dfrac{G(2m_{1})(2m_{2})}{4r^{2}}=\dfrac{Gm_{1}m_{2}}{r^{2}}$

i.e. force will remain the same.

5. A body is weightless at the centre of the earth. Why? 

Ans. At the centre of the earth g = 0

$\therefore W=mg=0$

6. Where will a body weigh more at Delhi or Shimla? Why?

Ans. We know that Shimla is a high-altitude mountain area so, the body will weigh more at Delhi because at higher altitudes the value of g decreases.

7. On which fundamental law of physics is Kepler’s second law based? 

Ans. Kepler’s second law is based on the law of conservation of angular momentum.

8. Which is greater: the attraction of the earth to 1 kg of aluminium or the attraction of 1kg of aluminium to the earth?

Ans. Following the universal law of gravitation both the forces are equal and opposite.

9. Distance between two bodies is increased to three times its original value. What is the effect of the gravitational force between them?

Ans. Since $F\varpropto\dfrac{1}{r^{2}}$

r’ → 3r 

Force will be decreased to 1/9 times.

10. What is Kepler’s law of periods? Show it mathematically?

Ans. It states that the square of the period of revolution of a planet around the sun is proportional to the cube of the semi-major axis of the elliptical orbit.

i.e., T2 ∝ R3 

T2 = KR3

where T is the period of evolution

R is the length of the semi-major axis

K is constant for all planets 

Section-B (2 Marks Questions)

11. Write three characteristics of gravitational force. 

Ans.

(1) It is a central force

(2) It obeys the inverse square law.

(3) It is a universal force and is always attractive.

12. Assuming Earth to be a uniform sphere, find an expression for the density of Earth in terms of g and G. 

Ans. Since $g=\dfrac{GM}{R^{2}}$

If the earth is a uniform sphere of mean density ρ 

$g=\dfrac{G}{R^{2}}\left ( \dfrac{4}{3}\pi R^{3}\rho  \right )$

$g=\dfrac{4}{3}\pi GR\rho$ 

$\Rightarrow \rho =\dfrac{3g}{4\pi GR}$

13. If the radius of the earth is 6400 km, what will be the weight of 1 quintal body if taken to the height of 1600 km above sea level?

Ans. R = 6400 km = 6400 × 103m 

h = 1600 km 

W = mg = 1 quintal = 100 kg = 100 × 10 =1000 N 

weight (w) = mgh

$W=mg\left ( \dfrac{R}{R+h} \right )^{2}$

$W=100\times 10\left ( \dfrac{6400}{1600+6400} \right )^{2}$

$W=640N=64\;kg$

14. Show that for a two-particle system $\vec{F}_{12}=\vec{F}_{21}$

Ans. $\vec{F}_{12}=\dfrac{Gm_{1}m_{2\hat{}}}{r^{2}}r_{21}$ (1)

$\vec{F}_{21}=\dfrac{Gm_{1}m_{2\hat{}}}{r^{2}}r_{12}$ (2)

From $\left ( \hat{}a=\dfrac{\vec{a}}{\left | \vec{a} \right |} \right )$

$\vec{F}_{12}=\dfrac{Gm_{1}m_{2}}{r^{3}}\vec{r}_{21}$

$\vec{F}_{21}=\dfrac{Gm_{1}m_{2}}{r^{3}}\vec{r}_{12}$

Since $\vec{r}_{12}=-\vec{r}_{21}$

$\vec{F}_{21}=\dfrac{-Gm_{1}m_{2}}{r^{3}}\vec{r}_{12}$

$\vec{F}_{21}=-\vec{F}_{12}$

Hence proved.

15. State two essential requisites of a geostationary satellite.

Ans. 

(1) The period of revolution of a satellite around the earth should be the same as that of the earth about its axis (T = 24 hrs)

(2) The sense of rotation of a satellite should be the same as that of the earth about its axis i.e., from west to east in the anti-clockwise direction.

16. A 400 kg satellite in a circular orbit of radius 2RE about the earth calculates the kinetic energy potential energy and total energy of the satellite.

RE = 6.4 × 106m

M = 6 × 1024kg

Ans. ME = 6 × 1024 kg, ms = 400 kg

RE = 6.4 × 106m 

Hence r = 2RE = 12.8 × 106m 

G = 6.67 × 10-4 Nm2/kg2

$KE=\dfrac{GM_{E}m_{s}}{2r}=\dfrac{6\cdot 67\times 10^{-11}\times 6\times 10^{24}\times 400}{2(12\cdot 8\times 10^{6})}$

$KE=6\cdot 25\times 10^{9}\;joules$

$P\cdot E=\dfrac{-2GM_{E}m_{s}}{2r}=-2KE$

$PE=-2\times 6\cdot 25\times 10^{9}=-12\cdot 5\times 10^{9}\;joules$

$T\cdot E\cdot =K\cdot E\cdot +P\cdot E\cdot$ 

$T\cdot E\cdot =6\cdot 25\times 10^{9}-12\cdot 50\times 10^{9}$

$T\cdot E\cdot =6\cdot 25\times 10^{9}\;joules$

Important Topics of Class 11 Physics Chapter 7 Gravitation 

CBSE Class 11 Physics Chapter 7 Gravitation Formulas

1. Newton’s Law of Gravitation:
$F = G \frac{m_1 m_2}{r^2}$

Where F is the gravitational force between two masses $m_1$​ and $m_2$​, r is the distance between the two masses, and G is the gravitational constant ($6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2$).

2. Gravitational Potential Energy (U):

$U = - G \frac{m_1 m_2}{r}$​​
This represents the potential energy between two masses $m_1$​ and $m_2$​ separated by a distance r.

3. Gravitational Field Intensity (g):
$g = G \frac{M}{r^2}$
Where M is the mass of the body creating the gravitational field, and r is the distance from the centre of the mass.

4. Acceleration due to Gravity on the Surface of the Earth:
$g = \frac{GM}{R^2}$

Where M is the mass of the Earth, R is the radius of the Earth, and g is approximately $9.8 \, \text{m/s}^2$.

5. Escape Velocity ($v_e$):

$v_e = \sqrt{\frac{2GM}{R}}$
This is the minimum velocity required to escape the gravitational field of a planet.

6. Orbital Velocity ($v_o$):

$v_o = \sqrt{\frac{GM}{r}}$
This represents the velocity required to keep a body in orbit around a planet or star.

7. Kepler’s Third Law of Planetary Motion:

$T^2 \propto r^3$

Where T is the period of the orbit and r is the radius of the orbit.

8. Period of Satellite (T):
$T = 2\pi \sqrt{\frac{r^3}{GM}}$

This formula gives the period of a satellite orbiting a planet.

Importance of Physics Class 11 Physics Chapter 7 Gravitation Revision Notes 

• Clarifies key concepts like gravitational force and fields. The notes break down tricky ideas into simple explanations.

• Provides clear examples of real-world applications. These examples show how gravity works in everyday life.

• Includes practice problems to test and improve problem-solving skills. You can work on these problems to get better at applying the concepts.

• Summarises important information for easier review. Gravitation Class 11 Short Notes summaries help you quickly review the main points.

• Supports better retention of material. Well-organised notes help you remember the information more easily.

• Facilitates quick revision before exams. The layout makes it easy to review everything you need to know before a test.

• Connects theoretical knowledge with practical applications. The notes show how what you learn about gravity relates to real-life situations.

• Boosts overall understanding and confidence in the subject. Clear explanations and practice help you feel more confident about the material.

Tips for Learning the Class 11 Chapter 7 Physics Gravitation

• Start by getting a good grasp of the basics like gravitational force, fields, and potential energy. These are the core ideas you need to understand before diving into more complex stuff.

• Use drawings and pictures to see how gravity affects things and to make sense of concepts like gravitational fields and orbits.

• Practice solving different problems to get comfortable with the formulas and see how the concepts apply in various situations.

• Write down key points, Gravitation Class 11 Short Notes, and formulas in your own words. This helps you remember and review the material more easily.

• Connect what you learn to real-life examples, like how gravity makes things fall or how planets move. This makes the ideas more understandable.

• Try teaching someone else what you’ve learned. It’s a great way to solidify your understanding and spot any gaps in your knowledge.

• Regularly go over your notes and practice problems to keep everything fresh in your mind and strengthen your learning.

Conclusion 

The availability of Vedantu’s FREE PDF download notes for CBSE Class 11 Physics Chapter 7 - "Gravitation" is a remarkable asset for students. These notes offer a comprehensive and structured overview of a fundamental physics concept that extends its importance far beyond the classroom. Understanding gravitation is pivotal not only for academic excellence but also for comprehending the cosmos, celestial mechanics, and space exploration. These notes simplify intricate topics like the universal law of gravitation, Kepler's laws, and orbital motion, providing students with the knowledge and tools needed to explore the mysteries of the universe. Overall, these downloadable notes are a valuable resource, fostering a deeper appreciation for the forces that shape our world and beyond.

Related Study Materials for Class 12 Physics Chapter 7

Chapter-wise Links for Physics Notes For Class 11 PDF FREE Download

Related Study Materials Links for Class 11 Physics

Along with this, students can also download additional study materials provided by Vedantu for Physics Class 11–